中3数学

※旧メニュー（番号順）

新メニュー表示 タイトルのみ表示

NO.	イメージ	授業の内容	pdf
1		式の乗法・除法
2		展開① 積の形になっている式を、和の形にする事を展開するという。展開するで使える無敵の技は全部がけ。
3		展開②・４つの公式
4		展開③
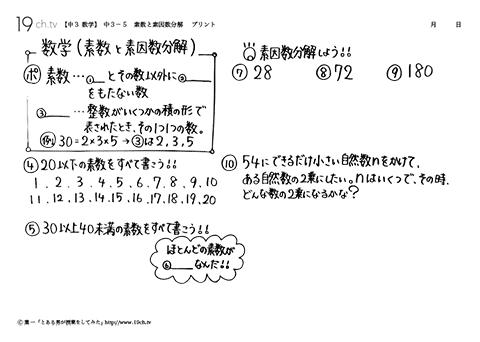
5		素数と素因数分解 素数・・・1とその数以外に約数をもたない数。因数・・・整数がいくつかの積の形で表されたとき、その1つ1つの数。
6		因数分解① 因数分解にも公式があるんだけどその前に覚えなきゃいけない技がくくり出し！！この技は、すべての項に入っている。数字や文字 を（　　）の前に出すこと。
7		因数分解②
8		因数分解③・ちょい応用編 もしくくり出しができるなら先にくくり出しをしてから因数分解しよう！
9		因数分解④・もっと応用編

中3数学 NO.10〜

NO.	イメージ	授業の内容	pdf
10		因数分解⑤・文章編
11		式の計算の利用①・くふう編
12		式の計算の利用②・代入編 式を整理してから代入しよう！！
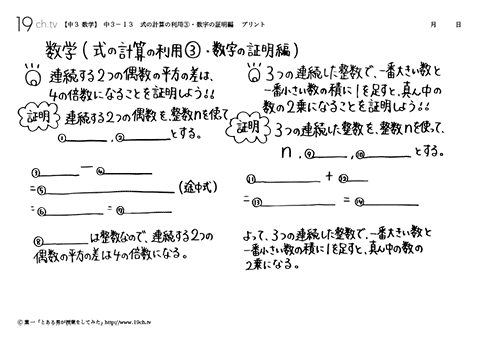
13		式の計算の利用③・数字の証明編 連続する2つの偶数の平方の差は、4の倍数になることを証明しよう！
14		式の計算の利用④・図の証明編 例題）縦の長さがm、横の長さがnの長方形のまわりに幅aの道がある。道の真ん中を通る線をlとするとき、道の面積がSがalに等しいことを証明しよう！！
15		平方根① 2乗するとaになる数をaの平方根という。√は根号といってルートと読む。
16		平方根② 整数を√に変形させるなら、2乗すればいい。
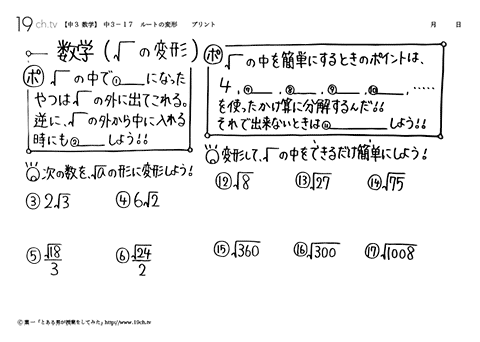
17		ルートの変形 √ の中を簡単にするときのポイントは、4、9、16、25、36を使ったかけ算に分解する。
18		ルートのかけ算・わり算 例題）②√3×√6=√18=3√2
19		有理化 √が分母いたら有理化しよう！！

中3数学 NO.20〜

NO.	イメージ	授業の内容	pdf
20		ルートのたし算・ひき算 √の中が同じもの同士しか計算できない。だから最初に√の中身チェックをしよう！！
21		ルートの計算のまとめ 例題）①3√2−8/√2+√72=5√2
22		ルートと展開のコラボ
23		ルートの問題をつめこんでみた
24		二次方程式①・基本編 ※（xの二次式）=0という形の方程式をxについての二次方程式という。解き方は、左辺の2乗を消して、右辺に±√をつける！！
25		二次方程式②・応用編
26		二次方程式③・解の公式編
27		二次方程式④・因数分解とのコラボ編
28		二次方程式⑤・まとめ編
29		二次方程式の利用①・正の整数編 例題）連続する2つの正の整数がある。それぞれを2乗した数の和が61のとき、この2つの数はいくつ？

中3数学 NO.30〜

NO.	イメージ	授業の内容	pdf
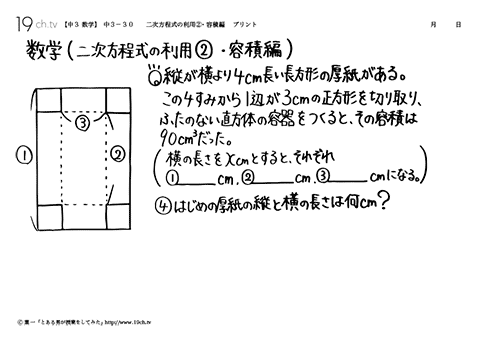
30		二次方程式の利用②・容積編 縦が横より4cm長い長方形の厚紙がある。この4すみから1辺が3cmの正方形を切り取りふたのない直方体の容器をつくるとその容積は90㎤だった...
31		二次方程式の利用③・面積編 例題）①面積が60㎡、まわりの長さが34mの長方形の縦と横は？
32		二次方程式の利用④・動点編 例題）点Pは辺AB上を毎秒1cmでAからBまで、点Qは辺AD上を毎秒2cmでDからAまで動く。P,Qが同時に出発するとき、何秒後に△APQの面積が24㎠になるかな？
33		二次関数って？ y=ax2で表されるとき『yはxの2乗に比例する』と いって、このときaを比例定数という。
34		二次関数の式をもとめる 例題）xとyの関係を式に表そう。yはxの2乗に比例しx=−2のときy=24。
35		二次関数のグラフ① y=ax2のグラフは、必ず原点を通る。そして、aが+だと上カーブ！aが−だと下カーブ！！
36		二次関数のグラフ② A〜Dの関数から当てはまるものをすべて書こう！A：y=3x2、B：y=−1/5x2、C：y=−x2、D：y=2/3x2
37		二次関数の変域 例題）yの変域をもとめよう！② y=3x2（1≦x≦3） のとき。
38		二次関数の変化の割合 y=ax2について、xの値がbからCまで増加したときの変化の割合はa（b+C)でもとめよう！
39		二次関数の利用①・平均の速さ編 例題）①xとyの関係を式に表すと？y=ax2　20=4a→a=5y=5x2ほか。

中3数学 NO.40〜

NO.	イメージ	授業の内容	pdf
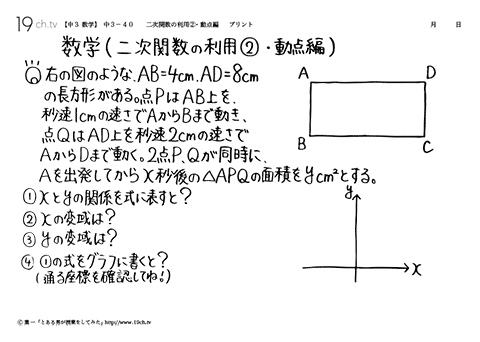
40		二次関数の利用②・動点編 ①xとyの関係を式に表すと？y=2X×X×1/2y=X2
41		二次関数の利用③・一次関数とのコラボ編 例題）②点Bの座標は？y=1/2×4=2（2、2）
42		二次関数の利用④・一次関数との交点編 右の図のようにy=x2とy=x+6が2点A、Bで交わっている。交点
43		相似って？ 2つの三角形が相似であるとき△ABC記号∞△DEF と表す。そして相似比は5：3で∠Aと∠Dの大きさは同じ。
44		三角形の相似条件① 相似条件は3つ！１、3組の辺の比がすべて等しい。２、2組の辺の比とその間の角がそれぞれ等しい。３、2組の角がそれぞれ等しい。
45		三角形の相似条件② 例題）①△ABCと相似な三角形をすべて書こう。△DBA、△DAC
46		相似の証明チャレンジ・Ｌｖ.１ 例題）∠BAC=90°の△ABCでAから辺BCに垂線ADをひくとき、△ABC∞△DBAであることを証明しよう。
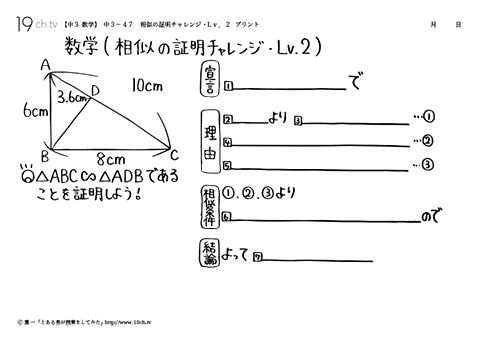
47		相似の証明チャレンジ ・Ｌｖ.２ △ABC∞△ADBであることを証明しよう！
48		相似の証明チャレンジ ・Ｌｖ.３ △DBF∞△FCEであることを証明しよう
49		平行線と線分の比①・基本編 ①x、yの値をもとめよう！x：5=4：6　6x=20　x=20/6=10/3cm

中3数学 NO.50〜

NO.	イメージ	授業の内容	pdf
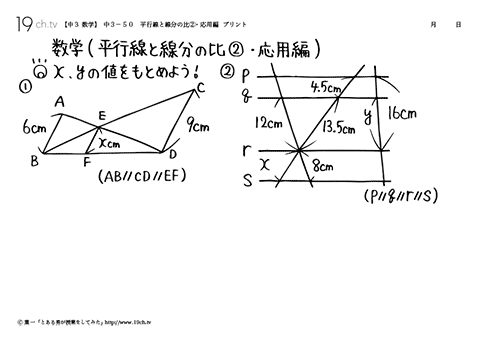
50		平行線と線分の比②・応用編 ①x、yの値をもとめよう！　x：9=2：5　5x=18　x=18/5cm
51		平行線と線分の比③・中点連結定理編 上の図のように点M、Nが辺AB、ACの中点のとき、MN//BCとなりMN：BC=1：2と なる。
52		相似と面積①・基本編 この2つの三角形の相似比は4：3で面積比は16：9
53		相似と面積②・応用編 ①△BOCの面積は？（1：9）　5×9=45㎠（1：9=5：x）
54		相似と体積①・基本編 相似である2つの円柱の相似比は3：2、表面積比は9：4、体積比は27：8！
55		相似と体積②・応用編 高さ12cmの円錐形の容器に56㎤の水を入れて、水面と上の面を平行にして深さを測ると8cmでした...
56		円周角の定理①・基本編 ∠x、∠yを求めよう！①x=27×2　x=54°
57		円周角の定理②・少し応用編 ∠x、∠yを求めよう！　①x=105°
58		円周角の定理 ③・もっと応用編 ∠x、∠yを求めよう！（①、②のl、mは円0の接線）①x=110°　②x=20°
59		円周角の証明チャレンジ・Ｌｖ.１ 例題）∠ABD=∠CBDのとき△ABE∞△DBCであることを証明しよう！

中3数学 NO.60〜

NO.	イメージ	授業の内容	pdf
60		円周角の証明チャレンジ・Ｌｖ.２ 例題）AB=CDのとき△ABE≡△DCEであることを証明しよう！
61		三平方の定理①・基本編
62		三平方の定理 ②・練習編 例題）①2辺の長さが4cm、8cmの長方形の対角線の長さは？
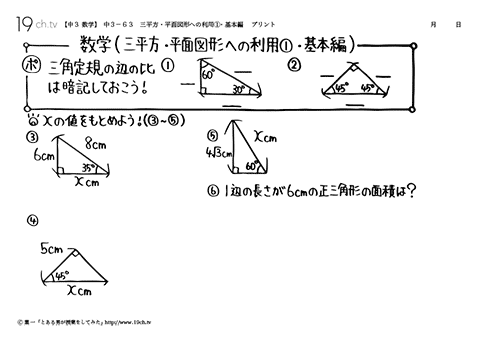
63		三平方・平面図形への利用①・基本編
64		三平方・平面図形への利用　②・面積編
65		三平方・平面図形への利用③・円とのコラボ編
66		三平方・平面図形への利用④・座標編
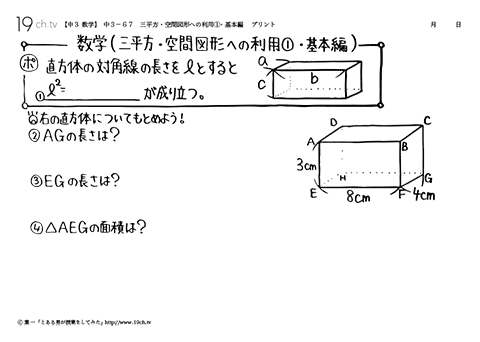
67		三平方・空間図形への利用① ・基本編
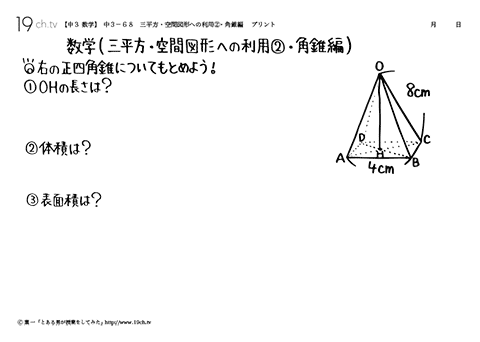
68		三平方・空間図形への利用②・角錐編 右の正四角錐についてもとめよう！
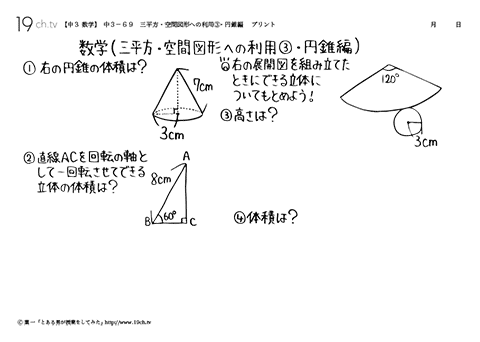
69		三平方・空間図形への利用③・円錐編 ①右の円錐の体積は？②直線ACを回転の軸として一回転させてできる立体の体積は？

中3数学 NO.70〜

NO.	イメージ	授業の内容	pdf
70		三平方・空間図形への利用④・長さが最小編 ①∠ABC=90°、AB=4cm、BC=5cm、AD=6cmの三角柱があり、BE上に点Pをとる。AP+PFの長さが最小になるとき、その長さは？
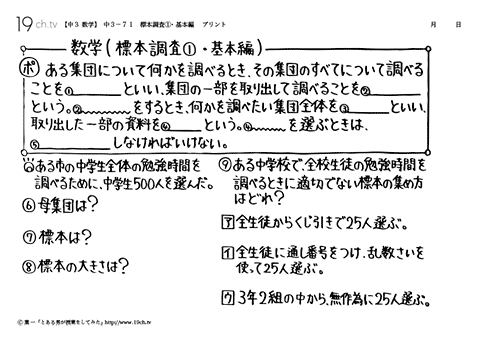
71		標本調査①・基本編 その集団のすべてについて調べることを全数調査といい、集団の一部を取り出して調べることを標本調査という。
72		標本調査②・問題編 人口18000人のA市で無作為に500人を抽出し、「好きなラーメンの味」についてアンケート調査した。このとき、A市すべての人のうち、みそ味が好きな人は、およそ何人？