とある男が授業をしてみた

中1・数学の授業

葉一の授業メニューと無料プリント

正の数・負の数 文字と式 方程式 関数 平面図形 空間図形 データの活用

旧メニュー表示

正の数・負の数

正の数・負の数 正の数・負の数の計算

正の数・負の数

	正の数・負の数① 負の数（ふのすう）とは、0よりも小さい数のこと。正の数（せいのすう）とは、0よりも大きい数のこと。整数（せいすう）とは、-4,12,0,9,+12、のような数。少数と分数が入らない。自然数（しぜんすう）とは、整数の中でも正になっているもの。
	正の数・負の数② 符号をつけて表すと、数直線、ことばを使って表す、例題（0より7小さい数）。
	正の数・負の数③ 数直線上で0からの距離を絶対値といいます。例題（3より5大きい数）、絶対値が3以下の整数をすべて書こうほか。

正の数・負の数の計算

	正負のたし算・ひき算 たし算（加法）、ひき算（減法）、交換法則、結合法則、最初に符号をチェックして、たし算にするのか、ひき算なのかを判断して計算しよう。
	（　）の無いたし算・ひき算 加法だけの式、（　）の無い計算のやり方、項、正の項、負の項。
	正負のかけ算・わり算① 正負のかけ算（乗法）・正負のわり算（除法）、乗法とは、かけ算のこと。除法とは、わり算のこと。
	正負のかけ算・わり算② 逆数、分数を含む正負のかけ算、分数を含む正負のわり算、分数、小数、かけ算、わり算を含む計算。
	指数 指数とは数字や式の右上に小さく書く記号（数字）のこと。指数は一番最初に計算する。間違いやすい指数は確実に覚えよう。
	計算のまとめ 加法、減法、乗法、除法まとめて四則という。 計算の順序は 指数→（　）の中→乗・除→加・減 （5+4）×（-3）を5×（-3）+4×（-3）のようにすることを分配法則という！
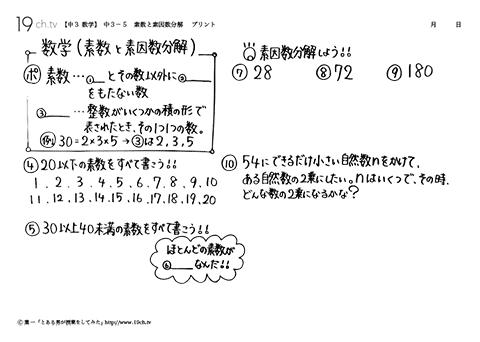
	素数と素因数分解（旧中3） 素数・・・1とその数以外に約数をもたない数。因数・・・整数がいくつかの積の形で表されたとき、その1つ1つの数。
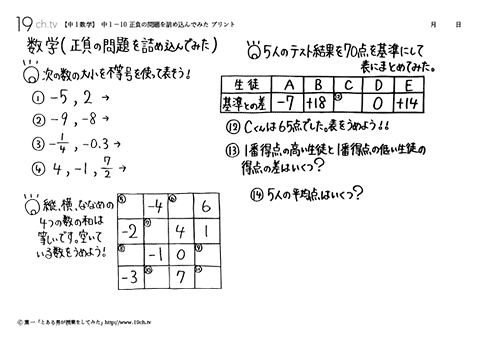
	正負の問題を詰め込んでみた 大小を不等号を使って表す、表をうめよう、正負の問題。例題 ・縦、横、ななめの4つの数の和は等しいです。空いている数をうめよう。

【中1数学】1章を52分で 4つの数・絶対値・マイナスのある計算・指数・素因数分解。

4つの数, 絶対値, マイナスのある計算, 指数, 素因数分解,

文字と式

文字と式 文字式の計算 文字式の利用

文字と式

	文字を使うときのルール 文字を使うときのルール。×、÷は書かない。文字より数字が先。文字はアルファベット順にする。同じ文字のかけ算は指数。。
	文字式を作ろう①～お金編～ 問題に慣れるまでは、 文章に線をひきながら解こう。例題：1本150円のジュースをx本買ったときの代金は？
	文字式を作ろう②～みはじ編～ 例題）時速5kmで、x時間歩いたときの道のりは？bkmの道のりを、2時間かけて歩いたときの速さは？
	文字式を作ろう③～割合編～ 1割は10％。例題）定価x円の品物を定価の25％引きで買ったときの代金は？
	文字式を作ろう④～色々編～ 例題）1辺がacmの正方形の周の長さは？9でわると商がxで、あまりが5になる数は？
	文字式を作ろう⑤～式の意味編～ それぞれの式は何を表している？　例題）ある映画館では、おとな1人x円、子供1人y円でチケットが売られている。

文字式の計算

	式の値 の中の文字とある数字をメンバーチェンジすることを代入という。例題）x=-3のとき、次の式の値は？
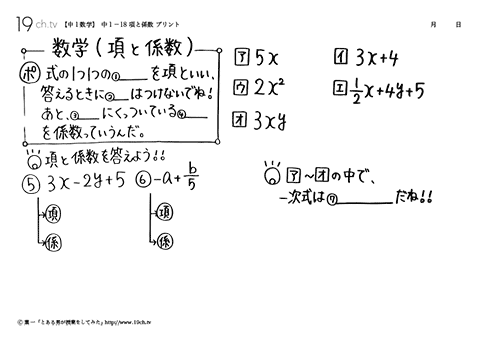
	項と係数 式の1つ1つのパーツを項といい、答えるときに+はつけないでね。あと文字にくっついている数字を係数という。項と係数を答えよう。
	文字式の加法・減法① 同じ文字だけ計算する。例題）5x−3x=　、−5a+12−3+5a=
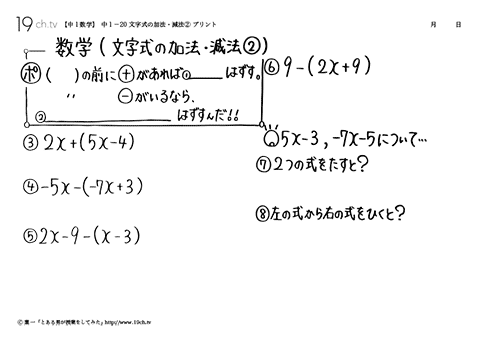
	文字式の加法・減法② （　）の前に+があればそのままはずす。（　）の前に−がいるなら、（　）の中の符号をかえてからはずす。例題）2x+（5x−4）=
	文字式と数の乗法・除法① （　）に×÷がくっついているなら、分配法則を使おう。
	文字式と数の乗法・除法② 分数の一から落ちたら、必ず（　）をつけよう。例題）5（x−2）−2（3x−1）=

文字式の利用

	関係を表す式① 3x+2y=2000のような式を等式といって=の左側を左辺、右側を右辺、あわせて両辺という。例題）1個x円のおかしを4個買うと代金はy円です。
	関係を表す式② 2x+5y＜3000のような式を不等式という。ちなみに、以上と以下のときは≦、≧ を使ってその数も含む意味。例題）ある数xから6をひくと、5より小さい。
	関係を表す式③ 例題）あるテーマパークの入場料は、おとな1人x円、子ども1人がy円です。このとき、次の式はどんなことを表しているかな？2x+3y=21100

方程式

方程式 方程式の利用

方程式

	方程式と解 3x+150=1200のように文字がある等式を方程式という。そして、その文字にあてはまる値を、解といってそれをもとめることを方程式を解くという。
	等式の性質 『方程式を解く』っていうのは、 左辺に文字だけを残すこと。例題）等式の性質を使って解こう。x+7=3
	方程式を解く①・基本編 『=』を飛びこえていく移項という技を使って左辺に文字の項を、右辺に数だけの項を集める。あと移項を使うと符号が変わる。方程式を解こう。例題）5x+7=4x+2
	方程式を解く②・（　）編 （　）があるときは、先に分配法則で（　）を消そう。 方程式を解こう。例題）3（x−4）=−2（x+1）
	方程式を解く③・小数と分数編 方程式を解こう。例題）0.2x−0.3=0.4x−0.1
	方程式を解く④・まとめ編 例題）10−（3x+4）=−x、3x+2a=1−2(x+a)の解が−3のとき、aの値はいくつ？
	比と比例式 比例式の解き方は、中中外外でかけ算する。例題）比の値はいくら？10：4

方程式の利用

	方程式の利用①・お金編 もとめたいものをxとおく。例題）ケーキを4個買って、120円の箱に入れてもらったら1400円でした。ケーキ1個の値段はいくら？
	方程式の利用②・あわせて編 例題）150円の梨と120円の桃をあわせて15個買うと、2070円でした、梨と桃をそれぞれ何個買ったかな？
	方程式の利用③・余りとたりない編 例題）何人かの子どもにあめを分けるのに6個ずつ分けると3個余り7個ずつ分けると9個たりない。子どもの人数とあめの個数は？
	方程式の利用④・長いす編 例題）長いす何脚が並べました。生徒が1脚に4人ずつ座ると7人が座れず、5人ずつ座ると3人だけ座った長いすが1脚できた。長いすの数と生徒数は？
	方程式の利用⑤・追いつく編 「み・は・じ」の問題は表を書こう。例題）兄が1800m離れたコンビに向かって家を出発した。それから10分後に、妹が兄が忘れたさいふを持って自転車で同じ道を追いかけた。
	方程式の利用⑥・２つの速さ編 例題）たくみ君は家から1920m離れた友達の家まで行くのに、はじめは分速120mで走り、途中から分速80mで歩いたので21分かかった。走った道のりと歩いた道のりは何m？
	方程式の利用⑦・時間差編 遅いときの時間−速いときの時間=時間差例題）A地点からB地点まで、行きは分速150mで走り、帰りは分速90mで歩いて帰ったら、かかった時間が8分違った。A地点からB地点までの道のりは何m？
	方程式の利用⑧・ある数編 例題)ある数nの5倍から8をひいた数が、nの3倍に6をたした数に等しくなる。ある数nの値はいくつ？
	方程式の利用⑨・昨年と今年編 昨年と今年の問題は表を書こう。例題)ある学校の昨年度の生徒数は300人でした。今年度は昨年度より男子が5％減って、女子が15％増えたので全体で13人増えた。
	方程式の利用⑩・比例式＋おまけ編 例題)4本で380円のジュースを14本買うといくら？、コーヒー80mlと牛乳200mlを混ぜてコーヒー牛乳を作る。同じ割合で作るとき、コーヒー100mlに何mlの牛乳を混ぜればいい？
	解が□であるとき 解が書いてあるなら、その数を文字に代入すればいい。例題）方程式−2+□=19+3xの解が−3のとき、□にあてはまる数は？

関数

関数 比例 反比例 比例・反比例の利用

関数

	関数って？ x、yのように、いろいろな値をとる文字を変数という。そして、xの値を決めると、それに対応してyの値がただ1つに決まるとき、yはxの関数であるという。あと、式に表すときは、y=の形で式に表そう。
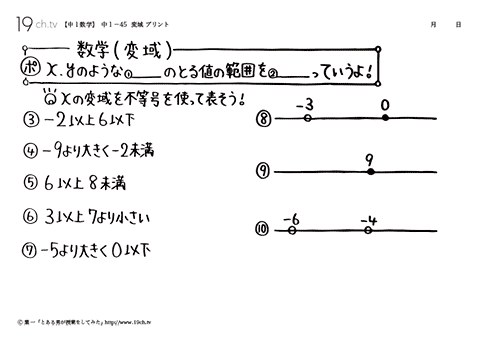
	変域 x、yのような変数のとる値の範囲を変域っていうよ。 例題）xの変域を不等号を使って表そう。−2以上6以下→−2≦x≦6

比例

	比例の式①・基本編 比例の式といえばy=ax。この式で表されるとき『yはxに比例する』という。また、このときのaを比例定数という。
	比例の式②・応用編 比例の式といえばy=ax! 例題）xとyの関係を式に表そう。1個130円の消しゴムをx個買ったときの代金をy円とする。
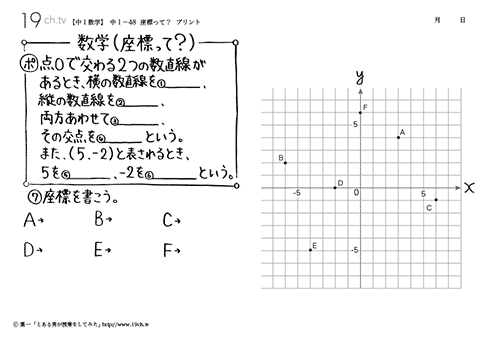
	座標って？ 点0で交わる2つの数直線があるとき、横の数直線をx軸、縦の数直線をy軸、両方あわせて座標軸、その交点を原点という。また、（5、−2）と表されるとき、5をx座標、−2をy座標という。
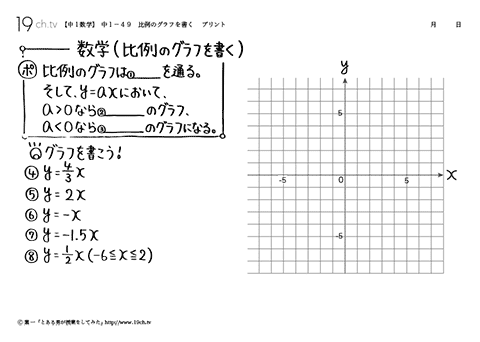
	比例のグラフを書く 比例のグラフは原点を通る。そして、y=axにおいてa＞0なら、右上がりのグラフa＞0 なら、左下がりのグラフになる。
	比例のグラフを読みとる グラフを読みとるときは、原点より右側で調べよう。例題）グラフを見て式を書こう。y=4x

反比例

	反比例の式①・基本編 反比例の式といえば、y=a/x。この式で表されるとき『yはxに反比例する』という。また、このときのaを比例定数という。
	反比例の式②・応用編 反比例の式といえばy= a/x。 例題）xとyの関係を式に表そう。50cmのリボンをx人に分けると、1人あたりのリボンの長さはycmである。
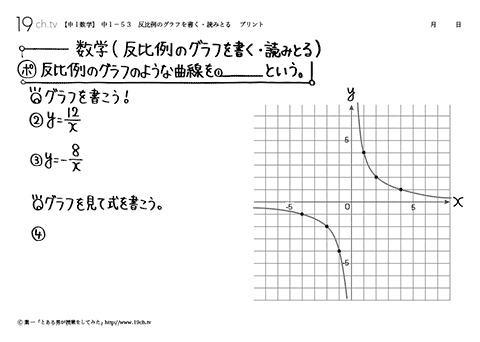
	反比例のグラフを書く ・ 読みとる 反比例のグラフのような曲線を双曲線という。 例題）グラフを書こう。y=12/x

比例・反比例の利用

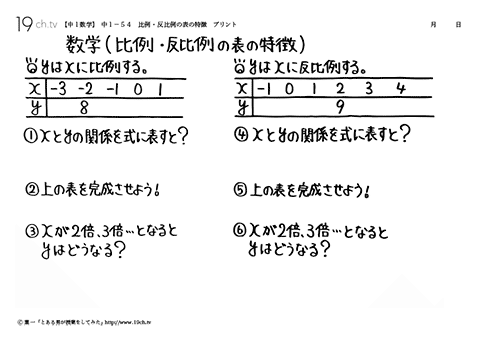
	比例 ・ 反比例の表の特徴 yはxに比例する。xとyの関係を式に表すと？y=ax→8=−2a、a=−4、y=−4x
	比例 ・ 反比例の利用①・基本編 例題）210cmのリボンをx人で分けると1人あたりのリボンの長さはycmになる。yをxの式で表すと？y=210÷x、y=210/x
	比例 ・ 反比例の利用②・圧力編 圧力は面積に反比例する。 圧力の単位はN/㎡を使う。例題）1500kgのものを、面積が10㎡の面で支える。このときの圧力は？
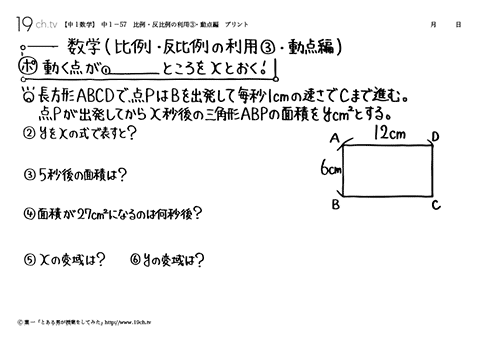
	比例 ・ 反比例の利用③・動点編 動く点が移動したところをxとおく！例題）長方形ABCDで点PはBを出発して毎秒1cmの速さでCまで進む。点Pが出発してからx秒後の三角形ABPの面積をY㎠とする。
	比例 ・ 反比例の利用④・水とロウソク編 例題）深さ40cmの容器があり、ここに水を8cm入れるのに10秒かかった。この割合で水をいれるとき、入れはじめからx秒後の水の深さをycmとする。
	比例 ・ 反比例の利用⑤・みはじの基本編 例題）Aさんの家からBさんの家まで毎分80mの速さで歩いていくと30分かかる。この道のりを毎分xmの速さでいくとy分かかるとする。
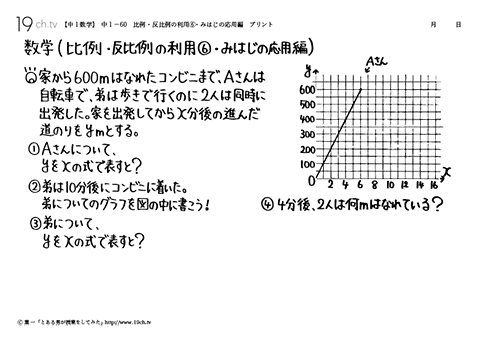
	比例 ・ 反比例の利用⑥・みはじの応用編 例題）家から600mはなれたコンビニまで、Aさんは自転車で、弟は歩きで行くのに2人は同時に出発した。家を出発してからx分後の進んだ道のりをymとする。
	比例 ・ 反比例の利用⑦・２つの水編 例題）150Lはいる浴そうに毎分6Lの割合でお湯を入れる。お湯を入れ始めてからx分後のお湯の量をyLとする。yをxの式で表すと？
	比例 ・ 反比例の利用⑧・歯車編 例題）Aの歯車の歯の数は56で、1分間に8回転する。Bの歯車の歯の数はxで、1分間にy回転する。yをxの式で表すと？
	比例 ・ 反比例の色々な問題 例題）yはxに比例し、x=6のときy=−5です。y=ax、−5=a×6、6a=−5→a=−5/6、x=−4のときのyの値は？

平面図形

直線と角 図形の移動と作図 円とおうぎ形の性質 おうぎ形の弧と面積

直線と角

	直線と角①・基本編 2点A、Bを通り、まっすぐに限りなくのびている線を直線ABAからBまでの部分を線分ABという。そして線分ABの長さを2点A,B間の距離という。
	直線と角②・問題編 例題台形ABCDについて！①平行な線分を記号を使って表すと？AD//BC

図形の移動と作図

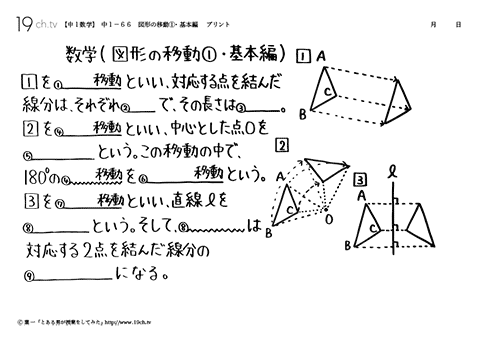
	図形の移動①・基本編 １を平行移動といい、対応する点を結んだ線分はそれぞれ平行で、その長さは等しい。２を回転移動といい、中心とした点0を回転の中心という。この移動の中で180°の回転移動を点対称移動という。
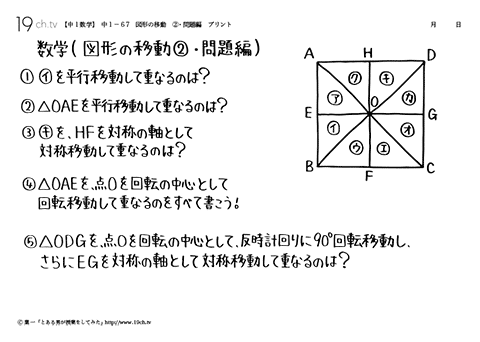
	図形の移動②・問題編 例題① イを平行移動して重なるのは？キ② △OAEを平行移動して重なるのは？△COF
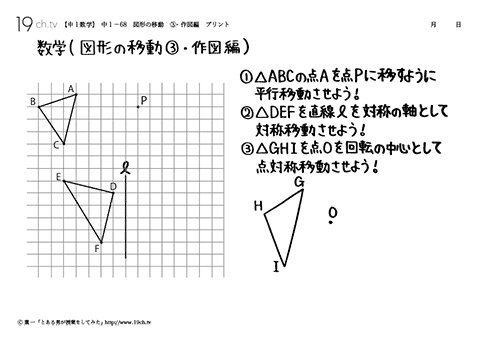
	図形の移動③・作図編 例題）①△ABCの点Aを点Pに移すように平行移動させよう！②△DEFを直線lを対処の軸として対称移動させよう！
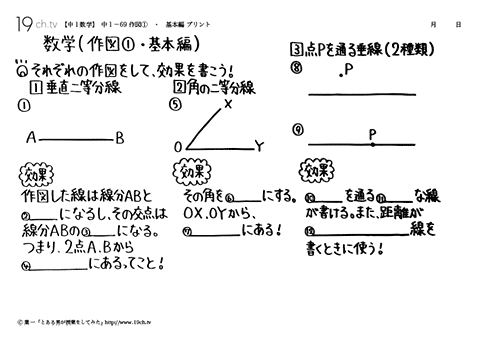
	作図①・基本編 垂直二等分線（効果）作図した線は線分ABと垂直になるし、その交点は線分ABの中点になる。つまり、2点A、Bから同じ距離にあるっってこと！角の二等分線（効果）その角を半分にする。OX、OYから同じ距離にある。
	作図②・応用編 例題）①△ABCにおいて辺ABの中点を作図しよう！②ABCにおいて、辺BCを底辺としたときの高さAHを作図しよう！
	作図③・さらに応用編 例題）①長方形ABCDにおいて、頂点Bが頂点Dに重なるように折るとき、折り目の線分を作図しよう！②2点A、Bから等しい距離にあり、かつ点Cにもっとも近い点Pを作図しよう！

円とおうぎ形の性質

	円とおうぎ形の性質①・基本編 １の図で、線分ABを弦AB、円周のAからBまでの部分を弧ABという。また、∠AOBを弧ABに対する中心角といい、線分ABが直径なら中心角は180°になる。
	円とおうぎ形の性質②・作図編 例題）①点Aが接点となるように接線 l を作図しよう！②中心が直線m上にあって、点Aで直線lに接する円を作図しよう！③割れた円形の皿の中心０を作図しよう！
	円とおうぎ形の性質③・おうぎ形編 右の図のOABをおうぎ形といい、∠AOBを中心角という。 例題）おうぎ形OABの面積が5π（パイ）㎠。③おうぎ形OCDの面積は？

おうぎ形の弧と面積

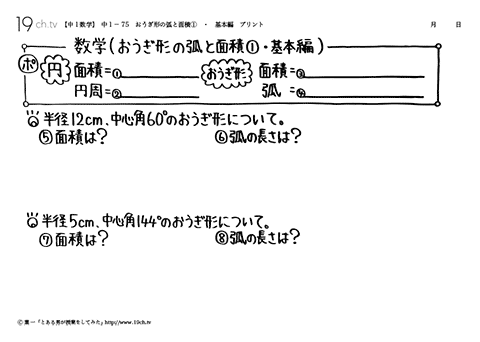
	おうぎ形の弧と面積①・基本編 円：面積=半径×半径×π、円周=直径×π 。 おうぎ形：面積=半径×半径×π×a/360、弧=直径×π×a/360 。
	おうぎ形の弧と面積②・応用編 例題）①半径9cm、面積36π㎠のおうぎ形の中心角の大きさと弧の長さをもとめよう！②半径6cm、弧の長さ9πcmのおうぎ形の中心角の大きさと面積をもとめよう！
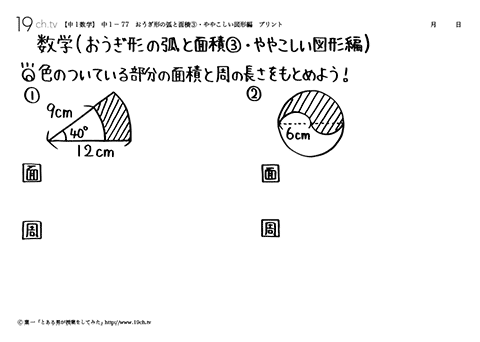
	おうぎ形の弧と面積③・ややこしい図形編 例題）色のついている部分の面積と周の長さをもとめよう！面積・周
	おうぎ形の弧と面積④・さらにややこしい図形編 例題）色のついている部分の面積と周の長さをもとめよう！面・周

空間図形

いろいろな立体 立体の見方 立体の表面積・体積

いろいろな立体

	いろいろな立体 赤の部分を底面、青の部分を側面、③を頂点という。ちなみに、いくつかの平面で囲まれた立体を多面体という。 例題）この立体の名前と底面と側面の名前は？
	空間内の平面と直線 ねじれの位置は平行と 交わるもの以外の残り物！！ 例題）辺ABと平行な辺は？辺ABと垂直に交わる辺は？辺ABとねじれの位置にある辺は？

立体の見方

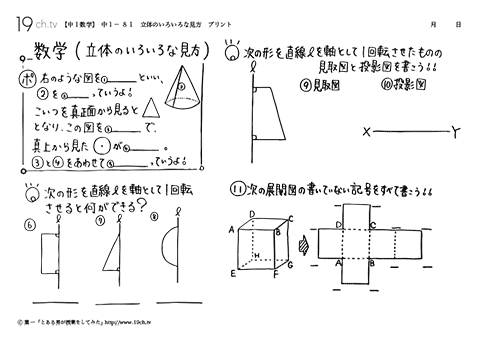
立体のいろいろな見方 右のような図を見取図といい、②を母線っていうよ。こいつを真正面から見ると△となり、この図を③立面図で、真上から見た図が④平面図◯③と④をあわせて投影図っていうよ。

立体の表面積・体積

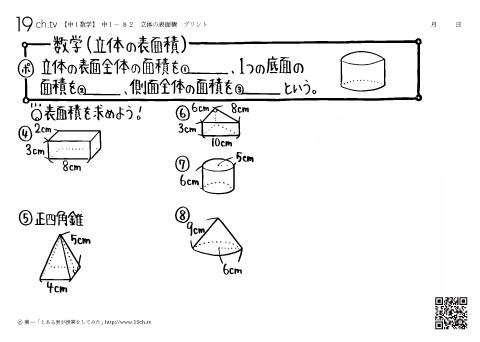
	立体の表面積 立体の表面全体の面積を表面積、1つの底面の面積を底面積、側面全体の面積を側面積という。例題）側面積と表面積をだそう！
	立体の体積 柱の体積=底面積×高さ、錐の体積=底面積×高さ×1/3 例題）体積を出そう！
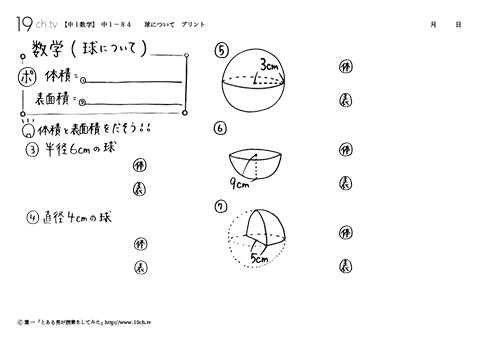
	球について ※体積=半径×半径×半径×π×4/3、表面積=半径×半径×π×4、 例題）体積と表面積をだそう！
	体積・表面積チャレンジ 直線lを回転の軸として、1回転させてできる立体の体積と表面積をだそう！

データの活用

データの分析と活用 確率

データの分析と活用

	度数分布 ①〜⑫をうめて度数分布表を完成させよう！⑬度数がもっとも多い階級は？
	代表値と散らばり 英単語10問テストをやりました！男子について⑤平均値は？⑥最頻値？⑦中央値は？⑧得点の範囲は？⑩最頻値は？最頻値はモード中央値はメジアン範囲はレンジともいう。
	資料の分析と活用まとめ 度数分布表、階級の幅、階級値、度数、相対度数、ヒストグラム、度数折れ線など。

確率

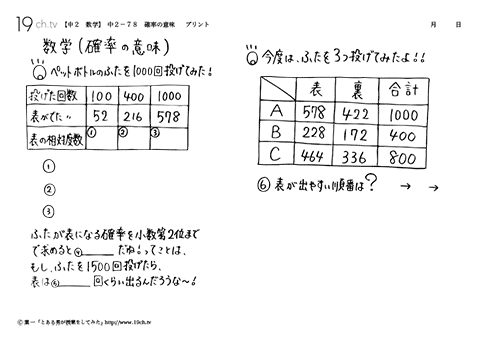
※（旧中2）は、中2から中1へ学習が移行したものです。

	確率の意味（旧中2） ペットボトルのふたを1000回投げてみた！ふたが表になる確率を少数第2位まで求めると...
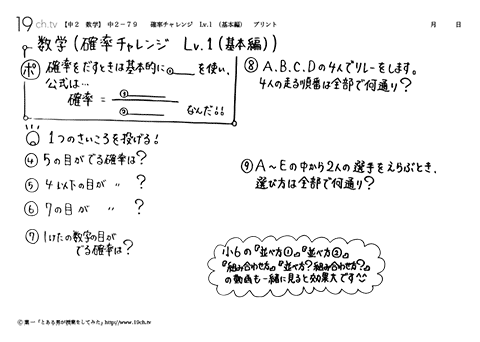
	確率チャレンジ　Lv.1（基本編）（旧中2） 確率をだすとき基本的に分数を使い公式は・・・確率=その数/全部