受験対策－数学3【図形】
高校受験対策－数学3【図形】の勉強動画ページ、無料プリント（PDF）のメニュー。高校受験対策 学習計画表 ? タイトルのみ表示
| NO.1 | イメージ | 授業の内容 | |
|---|---|---|---|
| 1 |  |
数学－図形① ①AB=AD、BF=12cm、DG=4cmのとき、四角形=BFDGの面積は？ |
|
| 2 |  |
数学－図形② 水が容器にふれている部分の面積を求めよう。 |
|
| 3 |  |
数学－図形③ ①∠ABE=54°のとき、∠BDCの大きさは？ |
|
| 4 |  |
数学－図形④ 線分ACと線分BDとの交点をEとする。 ①∠ACDの大きさは？ |
|
| 5 |  |
数学－図形⑤ 1辺の長さが4cmの立方体、①線分BHの長さは何cm？ |
|
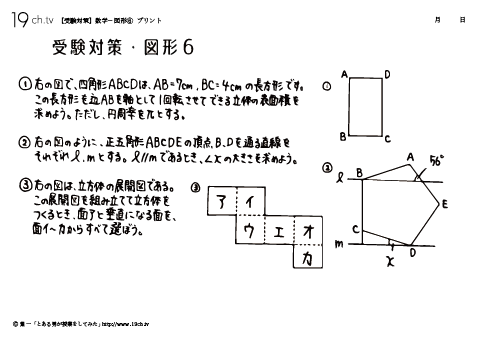
| 6 |  |
数学－図形⑥ 長方形を辺ABを軸として1回転させてできる立体の表面積を 求めよう。 |
|
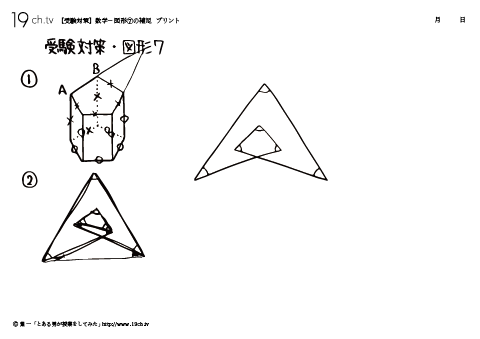
| 7 |  |
数学－図形⑦ 正五角柱において、辺ABとねじれの位置にある辺の数を求めなさい。 |
|
| 7b |  |
数学－図形⑦補足 ②右の図2で、印のあるすべての角の大きさの合計を求めなさい。 |
|
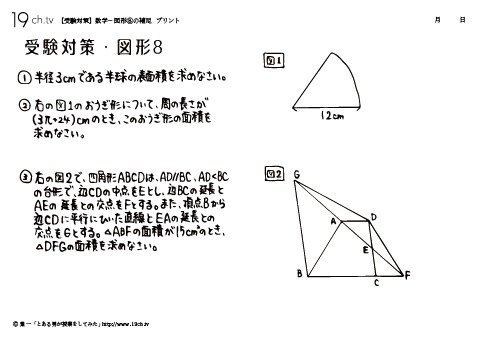
| 8 |  |
数学－図形⑧ 半径3cmである半球の表面積を求めなさい。 |
|
| 9 |  |
数学－図形⑨ 右の図1で、l//mのとき、∠x+∠yの大きさを求めなさい。 |
|
| 10 |  |
数学－図形⑩ 図1は、半径が6cmで中心角90°のおうぎ形と直角三角形を組み合わせたものである。 |
| NO. | イメージ | 授業の内容 | |
|---|---|---|---|
| 11 |  |
数学－図形⑪ 図はAB=3cm、BC=2cm、∠ABC=90°の直角三角形ABCを底面とし、点D を頂点とする三角錐 |
|
| 12 |  |
数学－図形⑫ 影をつけた部分の図形について①面積を求めよう。②周の長さを求めよ。 |
|
| 13 |  |
数学－図形⑬ ①点AからBまで、側面上を半周してひもをかけます。ひもの長さが最短になるときのひもの長さを求めなさい。 |
|
| 14 |  |
数学－図形⑭ 円錐の形をしたおもりがある。図1のようにおもりを倒し、すべらないように平面上を転がした。 |
|
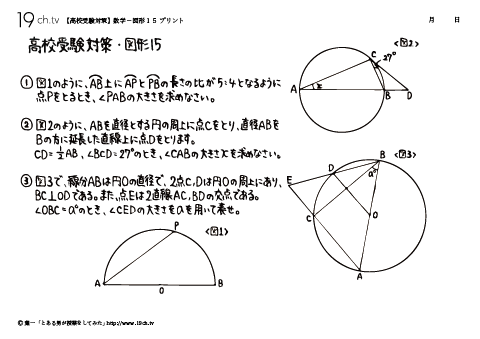
| 15 |  |
数学－図形⑮ ⌒AB上に⌒APと⌒PBの長さの比が5：4となるように点をとるとき、∠PABの大きさを求めなさい。 |
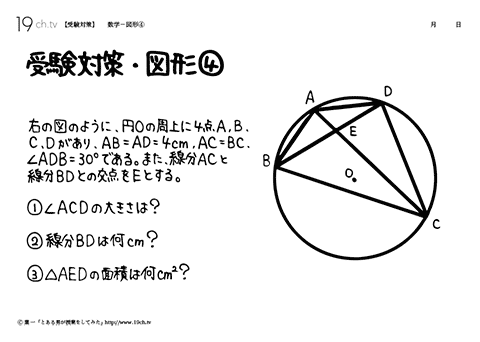
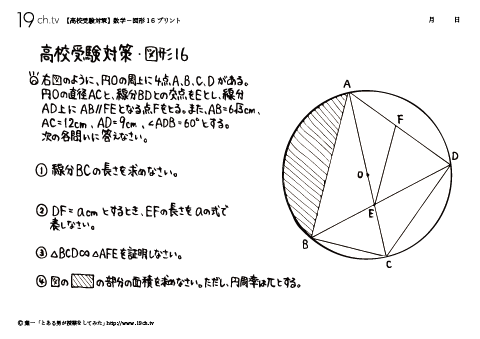
16 |  |
数学－図形⑯ 図のように、円Oの周上に4点A、B、C、Dがある。 |
| 17 |  |
数学－図形⑰ 図に示す立体において、辺BCとねじれの位置にある辺を、すべて書きなさい。 |
|
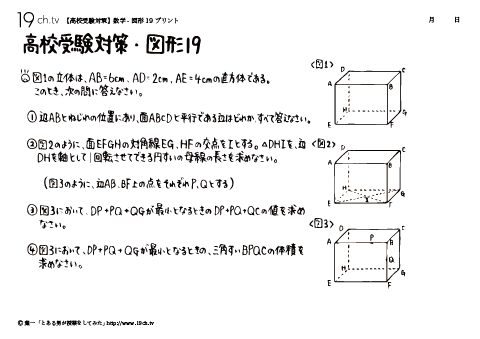
| 18 |  |
数学－図形18 図1の立体は、AB=6㎝、AD=2㎝、AE=4㎝の直方体である。このとき、次の問いに答えなさい。 |
|
| 19 |  |
数学－図形19 図1のような△ABCがあります。点D、Eはそれぞれ辺AB、BC上の点で、∠BDE=∠ACBです。AD=2㎝、DB=8㎝、BE=6㎝のとき、ECの長さを求めなさい。 |
|
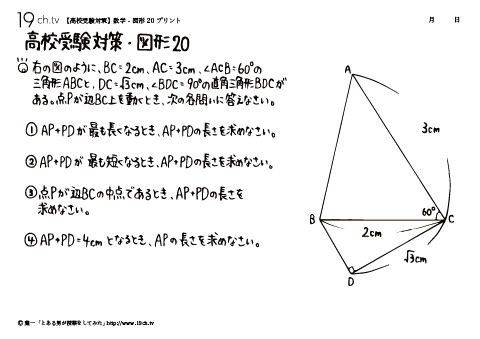
| 20 |  |
数学－図形20 右の図のように、BC=2㎝、AC=3㎝、∠ACB=60°の三角形ABCと、DC=√3㎝、∠BDC=90°の直角三角形BDCがある。点Pが辺BC上を動くとき、次の各問いに答えなさい。 |
| NO. | イメージ | 授業の内容 | |
|---|---|---|---|
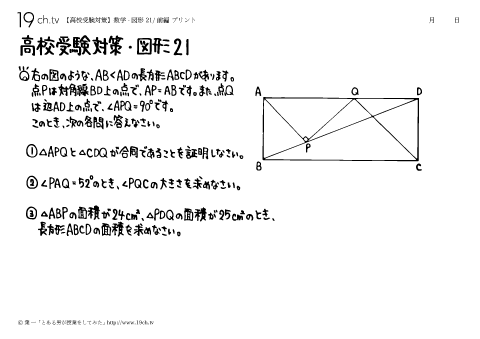
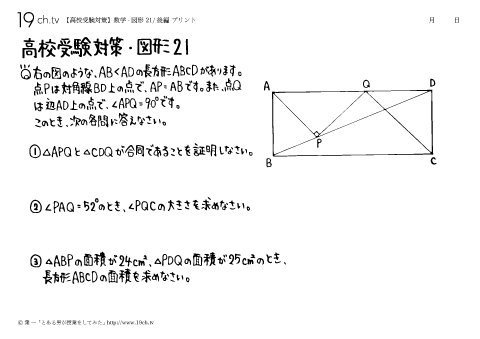
| 21a |  |
数学－図形21a 右の図のような、AB＜ADの長方形ABCDがあります。点Pは対角線BD上の点で、AP=ABです。また、点Qは辺AD上の点で、∠APQ=90°です。このとき、次の各問いに答えなさい。 |
|
| 21b |  |
数学－図形21b ①△APQと△CDQが合同であることを証明しなさい。②∠PAQ=52°のとき、∠PQCの大きさを求めなさい。③△ABPの面積が24cm²、△PDQの面積が25cm²のとき、長方形ABCDの面積を求めなさい。 |
|
| 22 |  |
数学－図形22 ①△ABEと△DCAが合同であることを証明しなさい。②∠BAC=40°、∠DAE=50°のとき、∠CBE、∠AEBの大きさをそれぞれ求めなさい。 |
|
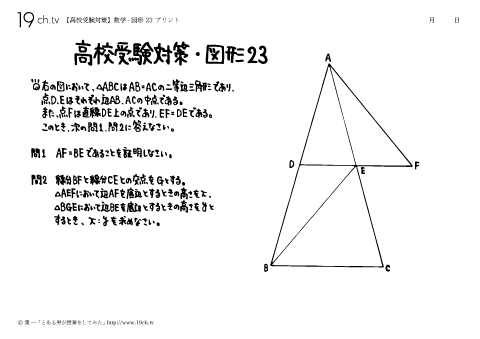
| 23 |  |
数学－図形23 △ABCはAB=ACの二等辺三角形であり、点D、Eはそれぞれ辺AB、ACの中点である。また、点Fは直線DE上の点であり、EF=DEである。このとき、次の問1、問2に答えなさい。 |
|
| 24 | 数学－図形24 青森の入試問題〜 |
||
| 25 | 数学－図形25 入試問題〜 |
||
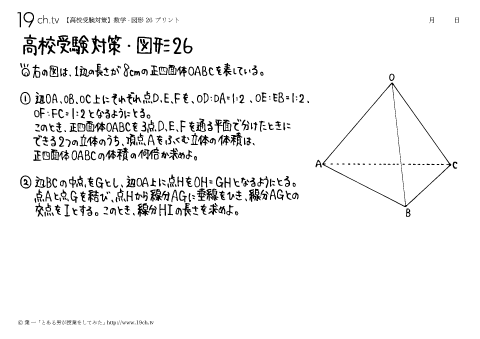
| 26 |  |
数学－図形26 右の図は、一辺の長さが8cmの正四面体OABCを表している。①辺OA,OB,OCにそれぞれ点D,E,FをOD:DA=1:2,OE:EB=1:2,OF:FC=1:2となるようにとる。 このとき、正四面体OABCを3点D,E,Fを通る平面で分けた時にできる2つの立体のうち、頂点Aを含む立体の体積は、正四面体OABCの体積の何倍か求めよ。 |
|
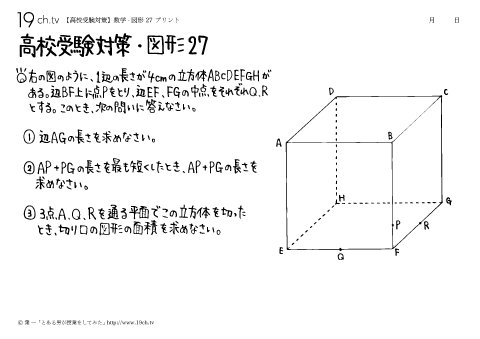
| 27 |  |
数学－図形27 右の図のように1辺の長さが4cmの立方体ABCDEFGHがある。辺BF上に点Pをとり、辺EF、FGの中点をそれぞれQ、Rとする。このとき、次の問いに答えなさい。 |
|
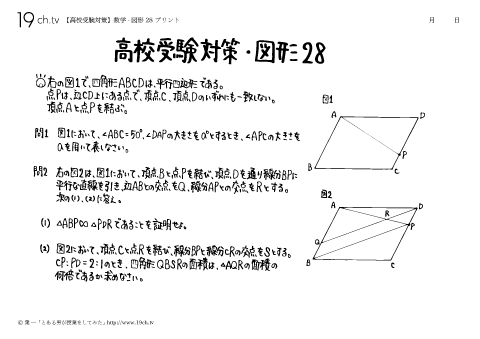
| 28 |  |
数学－図形28 右の図1で四角形ABCDは、平行四辺形である。点Pは辺CD上にある点で、頂点C、頂点Dのいずれにも一致しない。頂点Aと点Pを結ぶ。 問1：図1において、∠ABC=50°、∠DAPの大きさをa°とするとき、∠APCの大きさaを用いて表しなさい。 |
|
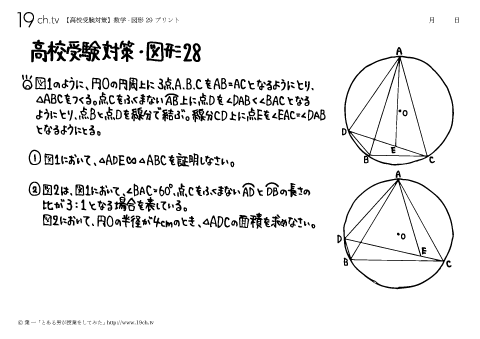
| 29 |  |
数学－図形29 図1のように、円Oの円周上に3点A.B.CをAB=ACとなるようにとり、△ABCをつくる。①図1において、△ADE∞△ABCを証明しなさい。 |
|
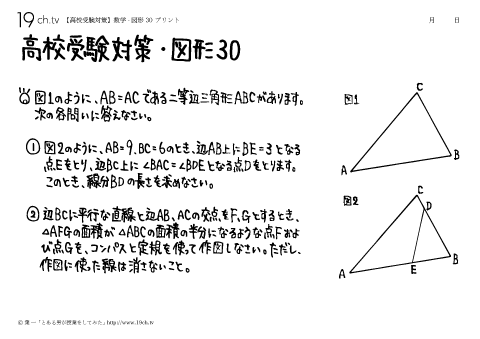
| 30 |  |
数学－図形30 図1のようにAB=ACである二等辺三角形ABCがあります。①図2のように、AB=9、BC=6のとき、辺AB上にBE=3となる点Eをとり、辺BC上に∠BAC=∠BDEとなる点Dをとります。このとき線分BDの長さを求めなさい。 |
| NO. | イメージ | 授業の内容 | |
|---|---|---|---|
| 31 |  |
数学－図形31 ①0≦X≦6のとき、四角形PBCQの面積をXを使って表せ。②6≦X≦12のとき、四角形PBCQの面積をXを使って表せ。 |
|
| 32 |  |
数学－図形32 ①△BEH∞△BADであることを証明せよ。 ②点Eから線分HFに垂線をひき、その交点をIとし、直線EIと辺BCとの交点をJとする。このときEH=FJであることを証明せよ。 |
|
| 33 |  |
数学－図形33 ①△ABC∞△DAFを証明せよ。②AB=10cm、BC=6cm、CA=8cmとするとき、線分FEの長さを求めよ。 |
|
| 34 |  |
数学－図形34 正三角形ABCが円に内接している。図のように点Aを含まない側の弧BC上に点PをとるときAP=BP+CPであることを証明せよ。 |
|
| 35 |  |
数学－図形35 ①線分EGと線分ECの長さをそれぞれ答えなさい。②線分MNの長さを求めなさい。③△ENMの面積を求めなさい。④三角すいBENMの体積を求めなさい。 |
|
| 36 |  |
数学－図形36 半円と複雑な回転体〜証明の問題、円の中の長さを求める問題、体積を求める問題 |
|
| 37 |  |
数学－図形37 平行四辺形の証明と面積。 |
|
| 38 |  |
数学－図形38 ライトが床を照らしてできる円の直径。yをxの式で表しなさい。またyの変域を求めなさい。2つのライトが照らしてできる円の面積が、等しくなるようなxの値を求めなさい。 |
|
| 39 |  |
数学－図形39 直角二等辺三角形の証明の問題、辺の長さを求める問題。 |
|
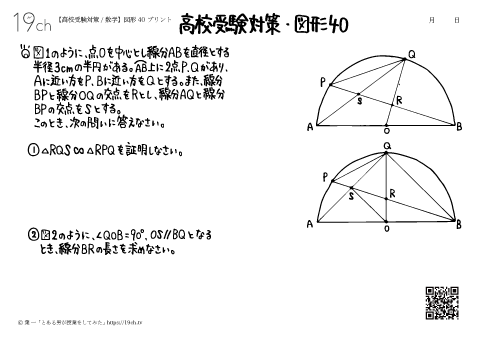
| 40 |  |
数学－図形40 相似の証明、線分の長さを求める問題。 |
| NO. | イメージ | 授業の内容 | |
|---|---|---|---|
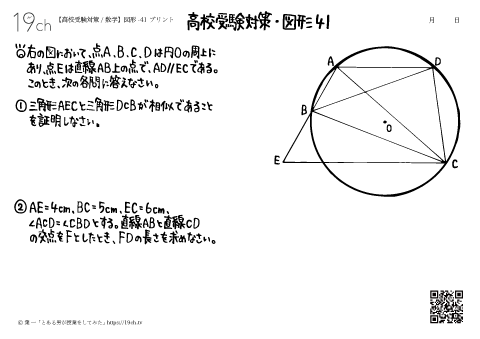
| 41 |  |
数学－図形41 ①三角形AECと三角形DCBが相似であることを証明しなさい。 ②直線ABと直線CDの交点をFとしたとき、FDの長さを求めなさい。 |
|
| 42 |  |
数学－図形42 おうぎ形の長さを求める問題。おうぎ形が入った長方形の長さを求める問題。 |
|
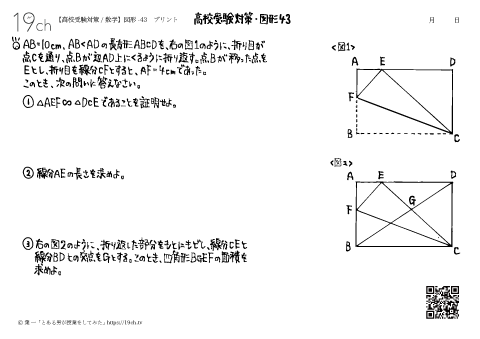
| 43 |  |
数学－図形43 長方形を折り目をつけた時の、角度の証明、線分の長さ、面積を求める問題。 |
|
| 44 |  |
数学－図形44 2つの円、接線と接点、証明、半径が3cmであるときの線分の長さを求めなさい。 |
|
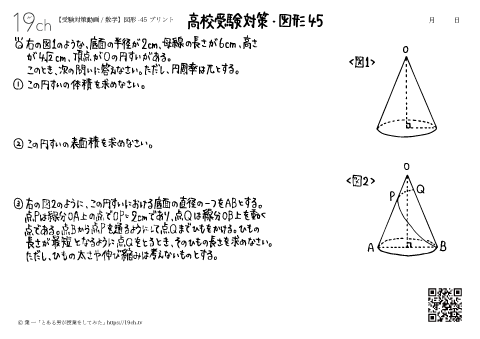
| 45 |  |
数学－図形45 円すいの周りの最短のひも！〜円すいの体積、円すいの表面積、円すいの周りのひもの長さを求める問題。 |
|
| - |  |
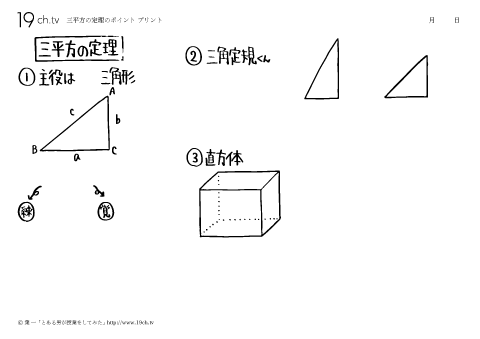
三平方の定理のポイント 受験前に三平方の定理の基礎を理解しておこう。 ①直角三角形 ②三角定規 ③立方体 |
ページ上部へ戻る