数Ⅲ

数Ⅲの勉強動画ページ、無料プリント（PDF）のメニュー。
　高校数Ⅲ 学習計画表 ? タイトルのみ表示

NO.	イメージ	授業の内容	pdf
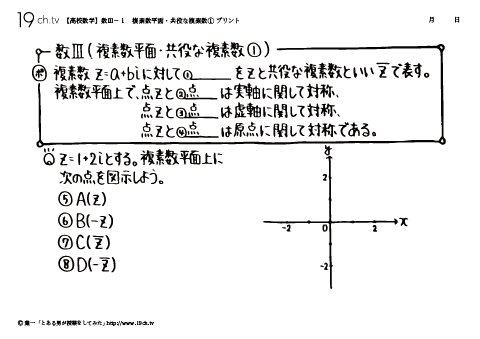
1		複素数平面・共役な複素数 複素数　Z=a+biに対して（1）a-biをZと共役な複素数という。
2		複素数平面・共役な複素数② 共役な複素数について次のことが成り立つ
3		複素数の絶対値・２点間の距離① 複素数Z=a+biに対して、√a2+b2をZの絶対値といい、|Z|で表し、 これは原点Oと点Zとの距離である。
4		複素数の絶対値・２点間の距離② 例題）α=3+(2x−1)i、β=x+2−iとする。2点A（α）、B（β) と原点Oが一直線上にあるとき、実数xの値を求めよ。
5		複素数の極形式① 複素数zの極形式、複素数zの②偏角
6		複素数の極形式② 例題）次の複素数の極形式で表そう。ただし、偏角θは0≦θ＜2πとする。
7		複素数の積と商① 0でない2つの複素数
8		複素数の積と商② 例題）αβ、α/βをそれぞれ極形式で表そう。
9		複素数の図表示① 点（√3+3i)zは、点zを原点０を中心にπ/3だけ回転し、原点からの距離を...

数Ⅲ NO.10〜

NO.	イメージ	授業の内容	pdf
10		複素数の積の図表示② 例題）複素数zに対して、点zを原点０を中心として5/6πだけ回転した点を表す複素数w1を求めよう。
11		複素数の積の図表示③ 例題）z1=√3+i、z2=2+2iのとき、積z1、z2を図示しよう。
12		ド・モアブルの定理① 整数nに対して（cosθ+isinθ)n=cosnθ+isinθ　次の値を計算しよう。
13		ド・モアブルの定理② 次の値を計算しよう。①(√3-i)4、②(1-i)-4
14		ド・モアブルの定理③ ①方程式Z3=−2√2iを解こう。
15		円と分点① 点A（α）、B（β）を結ぶ線分ABをm：nの比に内分する点はnα+mβ/m+n
16		円と分点② 次の等式を満たす点Zはどのような図形をえがくか。①｜z-3i|=2 ②｜z+5-2i|=4
17		円と分点③ 点Zが単位円の周上を動くとき、次のように表される点Wはどのような図形をえがくか。
18		複素数と三角形① 実数、鈍虚数
19		複素数と三角形② 3点P（2+i)、Q（3+2i)、R(x+3i)について、次の条件を満たすような実数X の値を求めよ。

数Ⅲ NO.20〜

NO.	イメージ	授業の内容	pdf
20		三角形の形状① 複素数β/αを求めよ。
21		三角形の形状② ①異なる3つの複素数Z1、Z2、Z3、の間に等式Z1+iZ2=(1+i)z3が成り立つとき 3点P(Z1)、Q(Z2)、R(Z3)を頂点とする△PQRはどのような三角形か。
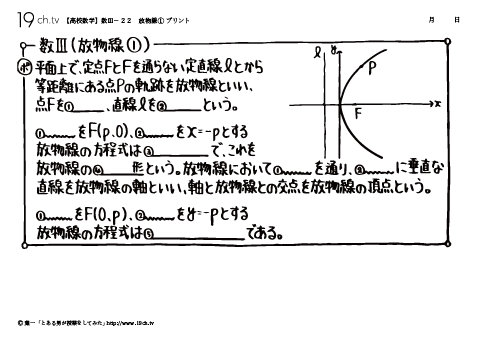
22		放物線① 焦点、準線、標準形
23		放物線② 放物線の焦点と準線を求めよ。放物線の方程式を求めよ。
24		放物線③ 点Aを内部に含まない円の中心の軌跡を求めよ。
25		楕円① 定点F、F'からの距離の和が一定である点Pの軌跡を楕円といい、点F、F'を焦点という。
26		楕円② 次の楕円の頂点と焦点を求めよ。
27		楕円③ 次の楕円の方程式を求めよ。
28		楕円④ x軸を基準にしてy軸方向に2/3倍して得られる図形の方程式を求めよ。
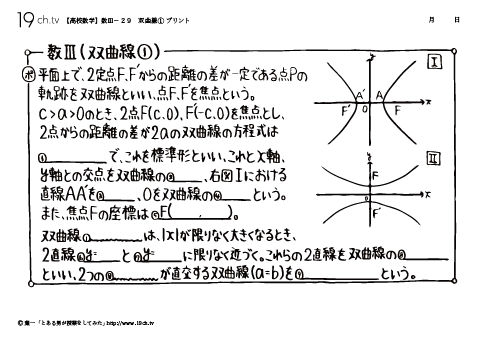
29		双曲線① y軸との交点を双曲線の頂点、右図Iにおける直線AA′を主軸、0を双曲線の中心という。

数Ⅲ NO.30〜

NO.	イメージ	授業の内容	pdf
30		双曲線② 次の双曲線の頂点と焦点および漸近線を求めよ。
31		双曲線③ 原点を中心とし、x軸またはy軸を主軸とする双曲線のうち、次の条件を満たすものの方程式を求めよ。
32		２次曲線の平行移動① 次の2次曲線をx軸方向に3、y軸方向に−2だけ平行移動した曲線の方程式と焦点を求めよ。
33		２次曲線の平行移動② 次の2次曲線の焦点を求めよ。①楕円4x2+9y2=24x
34		２次曲線の平行移動③ ①2点（−5、2）、（1、2）からの距離の和が10である点の軌跡を求めよ。
35		２次曲線と直線① ①双曲線x2-3y2=3と直線y=x+kの共有点の個数は、定数kの値によってどのように変わるか。
36		２次曲線と直線② 次の2次曲線の与えられた点における接線の方程式を求めよ。
37		２次曲線と直線③ 楕円2x2+y2=2と直線y=mx+2が接するように、定数mの値を求めよ。
38		２次曲線と直線④ ①点（4,1）から楕円x2+2y2=6に引いた接線の方程式を求めよ。
39		２次曲線と離心率 ①点F(1、0)と直線x=4からの距離の比が1：2であるような点Pの 軌跡を求めよ。

数Ⅲ NO.40〜

NO.	イメージ	授業の内容	pdf
40		曲線の媒介変数表示① 放物線y2=4px　x=pt2　y=2pt
41		曲線の媒介変数表示② θを媒介変数とする。次の式で表される図形はどのような曲線か。
42		曲線の媒介変数表示③ tを媒介変数とする。次の式で表される図形はどのような曲線か。
43		曲線の媒介変数表示④ ①x、yがx2/2+y2/8=1を満たす実数のとき、2x2+xy+y2の最大値、最小値を求めよ。
44		極座標と極方程式① 半直線OXを始線、角θを偏角という。 極座標に対して、x、y座標の組（x、y）を直交座標
45		極座標と極方程式② 次の極座標の点A、Bの直交座標を求めよ。
46		極座標と極方程式③ O を極とする極座標において、2点A（2、Π/6）、B（4、5/6Π）がある。
47		極座標と極方程式④ Oを極とする次の極方程式を直交座標で表される方程式に直せ。
48		極座標と極方程式⑤ 次の直交座標を用いて表された曲線を、極方程式で表せ。
49		極座標と極方程式⑥ 次の図形の極方程式を求めよ。ただし、Oは極とする。

数Ⅲ NO.50〜

NO.	イメージ	授業の内容	pdf
50		分数関数とそのグラフ① 次の関数のグラフをかけ。また、その漸近線を求めよ。
51		分数関数とそのグラフ② ①y=-2x+1/x−1②y=−2x+5/2x−1
52		分数不等式とグラフ ○次の不等式を解け。 ①3x+1/x−1＜x+2 ②3x/x+2≧2x−1
53		分数関数の決定 ①y= ax+b/x+cのグラフが点（2,1）を通り、2直線x=3、y=−2を漸近線とするとき、定数a、b、cの値を求めよ。
54		無理関数とそのグラフ① ○次の無理関数のグラフをかけ。①y=√3x ②y=ー√3x
55		無理関数とそのグラフ② ○次の無理関数のグラフをかけ。①y=√2-x　②y=ー√2x−4
56		無理不等式とグラフ ○次の不等式を解け。 ①√x−1＞x−3　②√−2x+7≦-x+2
57		無理方程式の解の個数 方程式√x+1=x+kが異なる2つの実数解をもつように、実数kの値の範囲を求めよ。
58		逆関数① 次の関数の逆関数を求め、その定義域と値域を求めよ。
59		逆関数② 次の関数の逆関数を求めよ。①y= log1/2x

数Ⅲ NO.60〜

NO.	イメージ	授業の内容	pdf
60		逆関数③ 次の関数の逆関数を求めよ。①y=3x−5/x−2（x＞2）
61		逆関数④ 次の関数の逆関数を求めよ。①y=x2-9（x≧0）
62		合成関数① yがuの関数でy=g(u)と表され、uがxの関数でu=f(x)と表されるとき、yはxの関数でy=g(f(x))と表され、これをfとgの合成関数という。
63		合成関数② ①f(x)=5x、g(x)=log5xであるとき、合成関数(gof)(x)、(fog)(x)を求めよ。
64		合成関数③ 2つの関数f(x)=ax-3、g(x)-x+aについて、(fog)(x)=(gof)(x)がつねに成り立つように、定数aの値を定めよ。
65		数列の極限① 次の数列の収束、発散を調べよ。①-3、-1、1、・・・2n-5、・・・
66		数列の極限② 次の極限を求めよ。①lim(-3n+8) n→00　②lim(n-1) n→00 ③lim (5+2/n) n→00
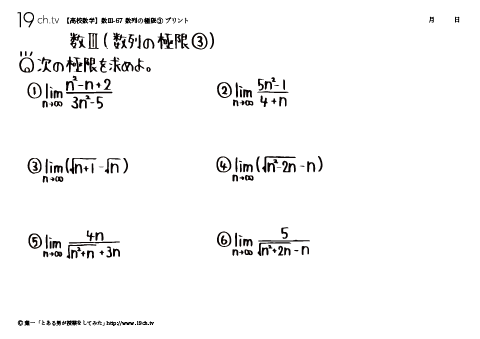
67		数列の極限③ 次の極限を求めよ。①lim n2-n+2/3n2-5 n→00 ②lim 5n2-1/4+n n→00
68		数列の極限④ はさみうちの原理 はさみうちの原理の問題、次の数列の極限を求めよ。①lim (-1)n/n+3
69		数列の極限⑤(無限等比数列) 次の数列の極限を求めよ。①lim3n、n→00

数Ⅲ NO.70〜

NO.	イメージ	授業の内容	pdf
70		数列の極限⑥ 無限等比数列 ①lim 1-rn/1+rn(rキ-1）、n→00
71		数列の極限⑦(無限等比数列) ①a1=1、an+1=1/3an+2（n=1、2、・・・・）によって定められる数列｛an｝についてlim anをもとめよ。
72		数列の極限⑧(無限級数) 次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
73		数列の極限⑨(無限等比級数) 次の無限級数の収束、発散を調べ、収束するときはその和を求めよ。
74		数列の極限⑩(無限等比級数) 次の無限級数が収束するような実数xの値の範囲と、収束するときの和を求めよ。
75		循環小数 次の循環小数を分数に直せ。
76		関数の極限① 次の極限を求めよ。①lim(x2-3x+1)
77		関数の極限② 次の等式が成り立つように、定数a、bの値を定めよ。①lim x2+ax+b/x+2=3
78		関数の極限③(右側左側) 次の極限を求めよ。①lim |x|/x　x→-0
79		関数の極限④ 次の極限を求めよ。①lim (32-5x+2)　x→00

数Ⅲ NO.80〜

NO.	イメージ	授業の内容	印刷用
80		関数の極限⑤(指数関数) 次の極限を求めよ。①lim (√2)x　x→00
81		関数の極限⑥(対数関数) 次の極限を求めよ。①lim log3x　x→00
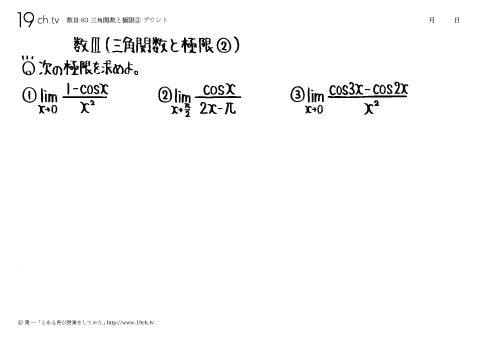
82		三角関数と極限① 次の極限を求めよ。①lim sin3x/x　x→0
83		三角関数と極限② 次の極限を求めよ。①lim 1-cosx/x2　x→0
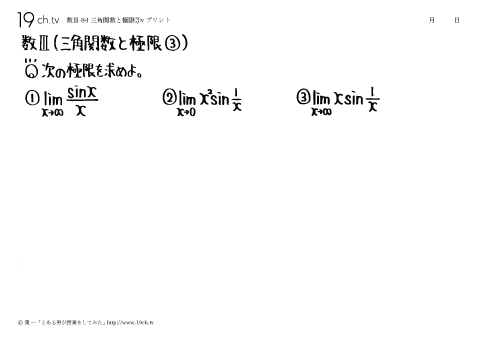
84		三角関数と極限③ 次の極限を求めよ。①lim sinx/x　x→00
85		関数の決定問題 式が成り立つように、定数a,bの値を定めよ。
86		関数の連続性① 次の不等式を満たす実数xの値の範囲を、区間で示す記号で示せ。
87		関数の連続性② 次の関数f(x)が、x-0で連続があるか不連続であるかを調べたよ。ただし【x】は、実数xを超えない最大の整数を表す。
88		関数の連続性③ ①関数f(x)=lim x2n+1/x2n +1のグラフをかき、f(x)が不連続となるxの値を求めよ。
89		中間値の定理 ①方程式x+log2x=2が1＜x＜2に少なくとも1つの実数解をもつことを示せ。

数Ⅲ NO.90〜

NO.	イメージ	授業の内容	印刷用
90		微分とは？ 関数f(x)の（　　）を求めることを微分という。 ○導関数の定義に従って、次の関数を微分せよ。
91		微分(復習編) 次の関数を微分せよ。①y=x4+x3+x2+x+1　②y=−2x3+7x+4
92		積の微分法 次の関数を微分せよ。 ①y=(x2+2x)(x+3) ②y=(5x2-3x−4）（2x+1）
93		商の微分法 次の関数を微分せよ。 ①y=2x/x2+1 ②y=1+x2/1-x2
94		合成関数の微分法① 次の関数を微分せよ。 ①y=(x2-5)3 ②y=(x3+3x)4
95		合成関数の微分法② 次の関数を微分せよ。①y=√x2-3x−1　②y=√(2x-3)3
96		三角関数の導関数① （sinx)'=①( 　　 )、（cosx)'=②( 　　 )、（tanx)'=③( 　　 )
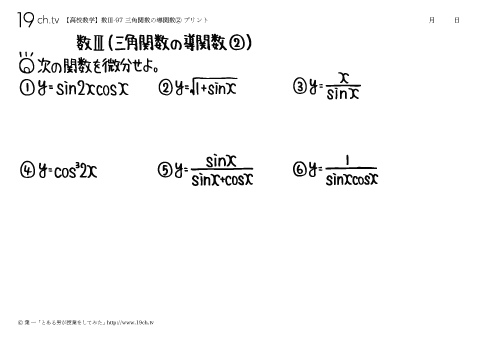
97		三角関数の導関数② 次の関数を微分せよ。①y=sin2xcosx、②y=√1+sinx、③y=x/sinx
98		対数関数の導関数① (logx)'①( 　 )、(logax)'=②( 　 )、(loga|x|)'=③( 　 )、(loga|x|)'=④( 　 )次の関数を微分せよ。⑤y=log6x。
99		対数関数の導関数② 次の関数を微分せよ。①y=(logx)2②y=logx/x

数Ⅲ NO.100〜

NO.	イメージ	授業の内容	印刷用
100		対数微分法 次の関数を対数微分法を用いて微分せよ。①y=x2 (x-1)/x-2②y=3√x2(x+1)
101		指数関数の導関数① 次の関数を微分せよ。③y=5x④y=3-x
102		指数関数の導関数② 次の関数を微分せよ。①y=exlogx②y=ex/ ex+e-x
103		高次導関数① 次の関数の第3次までの導関数を求めよ。①y=x4②y=sin2x
104		高次導関数② ①y=e-xのとき、y”+2y’+2y=0を示せ。②y=e2xsinxのとき、y”+ay’+by=0となるような定数a、bの値を求めよ。
105		高次導関数③ ①y=sinxのとき、y(n)=sin(x+nπ/2）(n=1,2,3,・・・）であることを証明せよ。
106		媒介変数表示された関数の導関数 ○xとyの関係が次の式で与えられるとき、dy/dxをtで表せ。①x=1/1+t2、y=t/1+t2
107		陰関数の導関数 ○x、yが次の式を満たすとき、dy/dxをx、yを用いて表せ。
108		接線と法線① 曲線y=f(x)上の点P（a,f(a)）におけるそれぞれの方程式は接線→①（　　　　　　）。法線→②（　　　　　　　）。
109		接線と法線② ①曲線y=tanx(0＜x＜π/2）について、傾きが2である接線の方程式を求めよ。

数Ⅲ NO.110〜

NO.	イメージ	授業の内容	印刷用
110		接線と法線③ 次の曲線上の点Ａにおける接線の方程式を求めよ。
111		接線と法線④(媒介変数表示編) 次の媒介変数で表された曲線において、（　　）内に示された曲線上の点における接線の方程式を求めよ。
112		接線と法線⑤(共通接線編) ①2つの曲線y=4/x、y=x2+kxが点Aで共通接線をもつように、定数kの値を求めよ。
113		平均値の定理① 次の関数f(x)と区間［a、b］に対して、条件 f(b)-f(a)/b-a=f’(c)、a＜c＜bを満たすcの値を求めよ。
114		平均値の定理② 次の不等式を平均値の定理を用いて証明せよ。①a＞0のとき1/a+1＜log（a+1）-loga
115		関数の増減 （1）f(x)=+3x4+4x3+12x2（2）f(x)=xlogx
116		関数の極値①
117		関数の極値②
118		関数の極値③ 次の関数の極値を求めなさい。①f(x)=x+2cosx　(0≦x≦π）②f(x)=sinx(1+cosx)　(0≦x≦2π）
119		関数の極限④ ①関数f(x)=x2eaxがx=1で極値をとるような定数aの値とそのときの極値を求めよ。

数Ⅲ NO.120〜

NO.	イメージ	授業の内容	印刷用
120		第２次導関数とグラフ① ④曲線y=x4-4x2x+1の凹凸を調べよ。
121		第２次導関数とグラフ② ①曲線y=x+1/xの概形を書け。
122		第２次導関数とグラフ③ ①曲線y=x2-3x+4/2x−2の概形を書け。
123		第２次導関数とグラフ④ ①x2-xyーy+x+2=0の漸近線を求めよ。 ②y=（logx)2概形を書け。
124		変曲点とグラフの対称性 曲線C：y=x3+3ax+bについて、次の問いに答えよ。 （1）Cの変曲点Pの座標を求めよ。（2）Cは点Pに関して点対称であることを示せ。
125		微分の不等式への応用① ①X>1のとき、不等式2√x>logXを証明せよ。
126		微分の不等式への応用② X>0のとき、不等式√1+X>1+1/2X-1/8X2を証明せよ。
127		微分の方程式への応用 aを定数とするとき、次のXにについての異なる実数解の個数を調べよ。 ①ex=X+a
128		速度と加速度①(直線上の点の運動編) 地上から真上に投げ上げた物体の時刻tにおける高さがh(t)=40t-5t2で表される時、次の問いに答えよ。 ①速度v(t)、加速度a(t)を求めよ。
129		速度と加速度②(平面上の点の運動編) 座標平面上を運動とする点P(x,y）の時刻tにおける座標がx=etcost、y=etsintであるとき、点Pの時刻tにおける速さと加速度の大きさをそれぞれ求めよ。

数Ⅲ NO.130〜

NO.	イメージ	授業の内容	印刷用
130		速度と加速度③(円運動編) 0が原点の座標平面上の動点Pの時刻における位置が、X=3cos2t、Y=3sin2tで表されるとき、次の問いに答えよ。
131		いろいろな量の変化率 ①毎秒3cm2の割合で表面積が増加している球がある。この球の半径が4cmになった瞬間における体積の変化率を求めよ。ほか。
132		近似式 X≒0のとき、次の関数について1次の近似式を求めよ。①√1+3x　②log(e+x)
133		不定積分①(準備運動編) 不定積分①(準備運動編)の問題、①∫5x2dx ②∫(8x3+x2-6x+5）dx
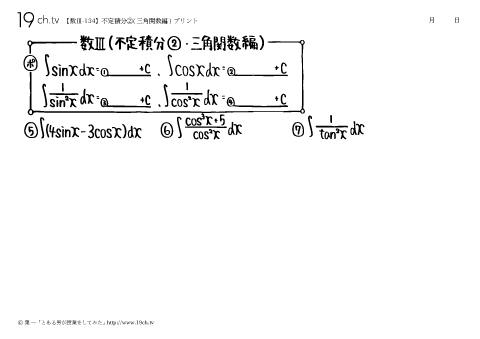
134		不定積分②(三角関数編) ①∫sinXdx=①（　　　　）+C　②∫cosXdx=②（　　　　）+C
135		不定積分③(指数関数編) ポイント、∫exdx=①（   ）+c、∫axdx=②（   ）+cほか。
136		置換積分① ①∫（4x-1)3dx　②∫sin(2θ+π/3）dθ　③∫3√2-x　dxほか
137		置換積分② ①∫x√x+1 dx、②∫（2x-1)(x+1)3dxほか。
138		置換積分③ ①∫(2x+1)(x2x-3）3dxほか
139		部分積分① ①∫xcosxdx ②∫（x+3)cos2xdx ③∫x2sinxdx

数Ⅲ NO.140〜

NO.	イメージ	授業の内容	印刷用
140		部分積分② ①∫xlogxdx ②∫log(x+2)dx ③∫(logx)2dx
141		分数関数の積分① 次の不定積分を求めよ。
142		分数関数の積分② 次の不定積分を求めよ。
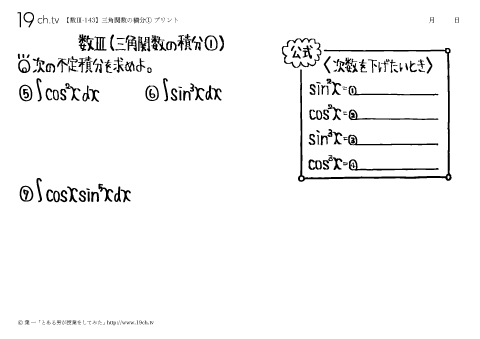
143		三角関数の積分① sin2x=（①  ）、cos2x=（②  ）、sin3x=（③  ）、cos3x=（③  ）
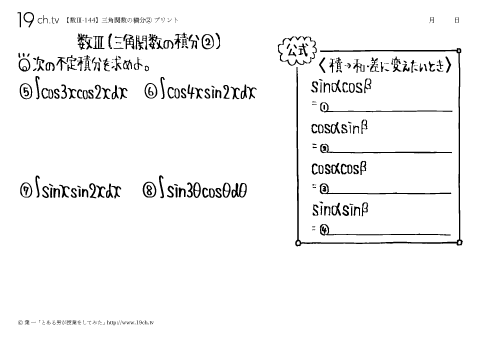
144		三角関数の積分② sinαcosβ、cosαsinβ、cosαcosβ、sinαsinβ
145		指数関数・対数関数の積分
146		積分特訓①
147		積分特訓②
148		積分特訓③
149		定積分①(基本編)

数Ⅲ NO.150〜

NO.	イメージ	授業の内容	印刷用
150		定積分②(絶対値編)
151		定積分③(レベルアップ編)
152		定積分の置換積分法①
153		定積分の置換積分法②(偶関数と奇関数)
154		定積分の置換積分法③
155		定積分の部分積分法①
156		定積分の部分積分法②
157		定積分の部分積分法③
158		定積分で表された関数①
159		定積分で表された関数②

数Ⅲ NO.160〜

160		定積分で表された関数③(極値編)
161		定積分で表された関数④(最大最小編)
162		区分求積法①
163		区分求積法②
164		定積分と不等式の証明
165		積分と面積①(基本編)
166		積分と面積②(やや複雑編)
167		積分と面積③(三角関数編)
168		積分と面積④(楕円編)
169		積分と面積⑤(媒介変数表示編)

数Ⅲ NO.170〜

170		積分と体積①(基本編)
171		積分と体積②(断面積編)
172		積分と体積③(放物線と直線編)
173		積分と体積④(媒介変数表示編)
174		曲線の長さ①(基本編)
175		曲線の長さ②(媒介変数表示編)
176		速度と道のり①(直線運動編)
177		速度と道のり②(平面運動編)

ページ上部へ戻る