高校数学（数A）

数Aの勉強動画ページ、無料プリント（PDF）のメニュー。
　高校数A 学習計画表 ? タイトルのみ表示

NO.	イメージ	授業の内容	pdf
1		集合① 9以下の自然数を全体集合とする。A=｛2、7、8｝、B｛1、2、4、7、9　｝について、次の集合を求めよう。
2		集合② 100から500までの自然数のうち、次のような数の個数を求めよう。
3		集合③ ①1から100までの自然数のうち、2、3、7の少なくとも1つで割り切れる数は何個ある？
4		場合の数①・基本編 ①1、1、1、2、3の中から、3個の数字を使ってできる3桁の整数は何通り？
5		場合の数②・正の約数編 ① 48の正の約数は何個？② 48の正の約数の総和はいくつ？
6		場合の数③・自然数の組編 ①x+2y+3z=11を満たす自然数の組（x、y、z）は何組ある？
7		順列①・基本編 ⑦5個の文字a、b 、c 、d、 eから異なる3個を選んで1列に並べるときの並べ方は何通り？
8		順列②・続・基本編 ① 5種類の数字1、2、3、4、5を並べて3桁の整数をつくると何通りできる？
9		順列③・男女編 男子3人と女子5人が1列に並ぶとき、次のような並び方は何通りある？

数A NO.10〜

NO.	イメージ	授業の内容	pdf
10		順列④・数字編 5個の数字1、2、3、4、5から異なる3個の数字を使って3桁の整数を作る時、次のような整数は何個作れる？
11		順列⑤・数字の応用編 5個の数字0、1、2、3、4から異なる3個の数字を使って 3桁の整数を作る。
12		順列⑥・じゅず順列編 ①8クラスの学級委員長が、円形の机に座るとき、着席の方法は何通り？
13		順列⑦・グループ分け編 ①10人をA、Bの2部屋に入れる方法は何通り？ただし、全部の人を1つの部屋に入れてもいい。
14		組み合わせ①・基本編 ⑦10人の生徒から3人を選ぶとき、選び方は何通り？
15		組合せ②・文字編 TAKASAKIの8文字すべてを1列に並べる。①全部で並べ方は何通り？
16		組合せ③・男女編 男子6人、女子4人の中から4人のメンバーを選ぶとき、次のような選び方は、それぞれ何通り？
17		組合せ④・道順編 右の図のような道で、AからBまで行くのに、次の場合の最短経路は何通り？
18		組合せ⑤・重複編 ①桃、みかん、梨の3種類の果物がたくさんあり、その中から6個の果物を買うとき、買い方は何通り？
19		確率①・さいころ編Part.1 3個のさいころを同時に投げるとき、次の場合の確率は？

数A NO.20〜

NO.	イメージ	授業の内容	pdf
20		確率②・さいころ編Part.2 3個のさいころを同時に投げるとき、次の場合の確率は？
21		確率③・さいころ編 Part.3 1個のさいころを6回投げるとき、次の場合の確率は？
22		確率④・さいころ編 Part.4 数直線上の原点0に点Pがある。さいころを1回投げることに、偶数の目が出たら数直線上を正の方向に3、奇数の目が出たら負の方向に2だけ進む。
23		確率⑤・色玉編 Part.1 袋の中に白玉5個、赤玉4個が入っている。ここから、玉を同時に5個取り出す。
24		確率⑥・色玉編 Part.2 袋の中に白玉6個、赤玉4個、青玉3個が入っている。ここから、玉を同時に4個取り出すとき、次の場合の確率は？
25		確率⑦・色玉編 Part.3 Aの袋には赤玉6個と白玉4個、Bの袋には赤玉4個と白玉6個が入っている。
26		確率⑧・色玉編 Part.4 ①白玉3個、赤玉6個の入っている袋から、玉を1個取り出し、色を調べてからもとに戻すことを7回繰り返すとき、7回目に3個目の白玉が出る確率は？
27		確率⑨・くじ編 当たりくじ3本を含む10本のくじがある。A、Bがこの順に1本ずつ1回だけ引くとき、次の確率を求めよう。
28		確率⑩・じゃんけん編 ①3人でじゃんけんを1回するとき、1人だけが勝つ確率は？
29		条件付き確率① 事象Aが起こったときに事象Bが起こる確率をAが起こったときのBの条件付き確率（PA(B))といいPA(B)=P(A∧B)/P(A)

数A NO.30〜

NO.	イメージ	授業の内容	pdf
30		条件付き確率② ①数本の当たりくじを含む10本のくじを、まずAが1本引き、もとにもどさずに、Bが1本ひくとき、2人がともに当たりくじを引く確率は2/15であった。当たりくじの本数を求めよう。
31		条件付き確率③ 3つの箱a、b、C、があり、それぞれに赤玉と白玉が右の表のように入っている。無作為に1組選んで1個の玉を取り出すとき、次の確率を求めよう。
32		条件付き確率④ ①製品が品質検査で不良品と判定される確率を求めよう。
33		内分・外分① 線分ABにおいて、次の点を記入しよう。
34		内分と外分② △ABCの∠Aの二等分線と辺BCの交点をPとする。→AB:AC=BP:PC
35		三角形の内心・外心・重心・垂心① 内心：三角形の3つの内角の二等分線は1点で交わる。外心：三角形の3つの辺の垂直二等分線は1点で交わる。
36		三角形の内心・外心・重心・垂心② ○点Iを△ABCの内心、点Oを△ABCの外心とするとき、 角x、yを求めよう。
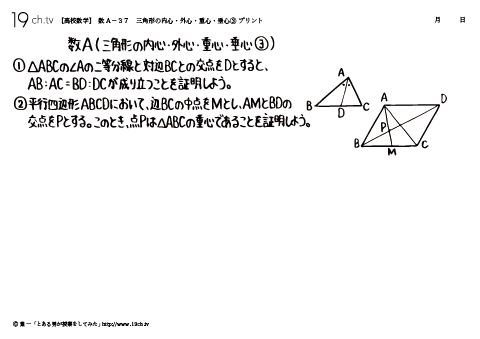
37		三角形の内心・外心・重心・垂心③ ①△ABC∠Aの二等分線と対辺BCとの交点をDとすると、AB:AC=BD:DCが成り立つことを証明しよう。
38		三角形の内心・外心・重心・垂心④ ①△ABCの内心をIとし、直線AIと辺BCの交点をDとする。AB=6、BC=5、CA=3であるとき、AI:IDを求めよう。
39		傍心と傍接円 三角形の1つの内角の二等分線と、他の2つの頂点における外角の二等分線は1点で交わる。この点を傍点という。

数A NO.40〜

NO.	イメージ	授業の内容	pdf
40		チェバの定理① △ABCの辺BC、CA、AB上にそれぞれ点P、Q、Rがあり、3直線AP、BQ、CRが1点で交わるとき
41		チェバの定理② 次の図において、AR:RBを求めよう。
42		メネラウスの定理① ある直線が△ABCの辺BC、CA、AB、またはその延長と、それぞれ点P、Q、Rで交わるとき　QC/AQ・PB/CP・RA/BR=1
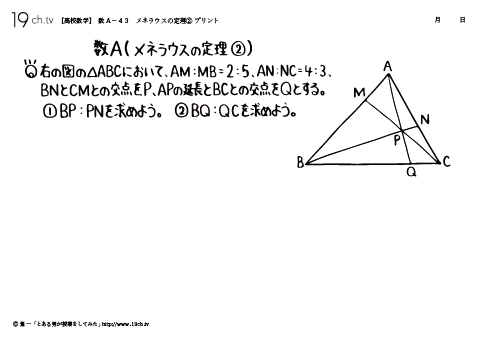
43		メネラウスの定理② 右の図の△ABCにおいて、AM:MB=2:5、AN:NC=4：3、BNとCMとの交点をP、APの延長とBCとの交点をQとする。
44		三角形の辺と角の大小関係 3辺の長さが次のような三角形は存在するかどうかを調べよう。
45		円周角の定理① 下の図について、∠Xの大きさを求めよう。
46		円周角の定理② ①右の図で、L、M、Nはそれぞれ、円に内接する四角形ABCDの辺AB,BC,ADの中点である。
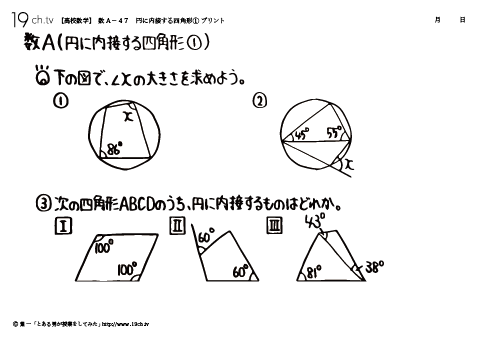
47		円に内接する四角形① 下の図で、∠xの大きさを求めよう。
48		円に内接する四角形② △ABCの頂点Aから、辺BCに垂線ADを引き、点Dから辺AB、辺ACにそれぞれ垂線DE、DFを引くと、4点E、B、C、Fは同一円周上にあることを証明しよう。
49		トレミーの定理 円に内接する四角形ABCDについて

数A NO.50〜

NO.	イメージ	授業の内容	pdf
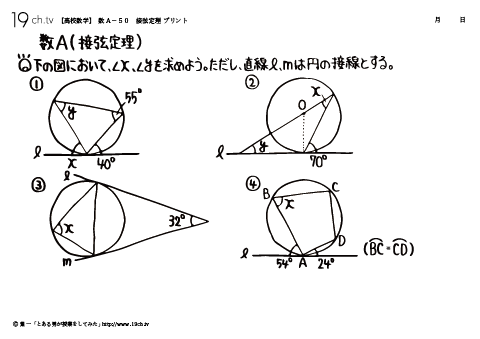
50		接弦定理 下の図において、∠X、∠Yを求めよう。
51		方べきの定理① 下の図でxを求めよう。ただし、Tは接点とする。
52		方べきの定理② BF:FC=m:nとするとき、BE・BDをr、m、nを用いて表そう。
53		方べきの定理③ 4点C、D、E、Fは同一円周上にあることを証明しよう。
54		２つの円の位置関係と共通接線① それぞれの半径がr、r’（r＞r’）である2つの円の中心間の距離をdとするとき、①〜⑤におけるr、r’、dの関係をかこう。
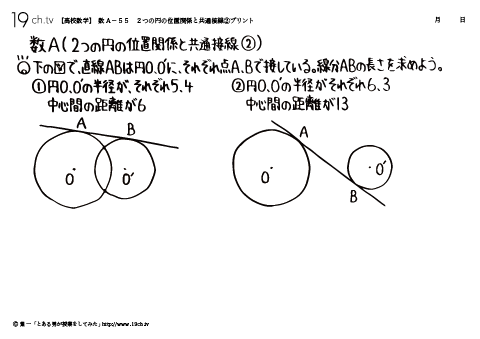
55		２つの円の位置関係と共通接線② 直線ABは円O、O'に、それぞれ点ABで接している。線分ABの長さを求めよう。
56		２つの円の位置関係と共通接線③ 2つの円がTで内接している。内側の円の接線が外側の円と交わる点をA、Bとし、その接点をPとする。
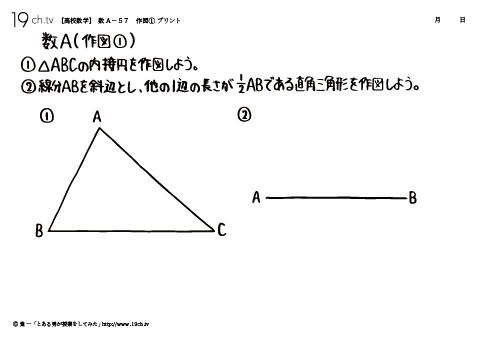
57		作図① △ABCの内接円を作図しよう。
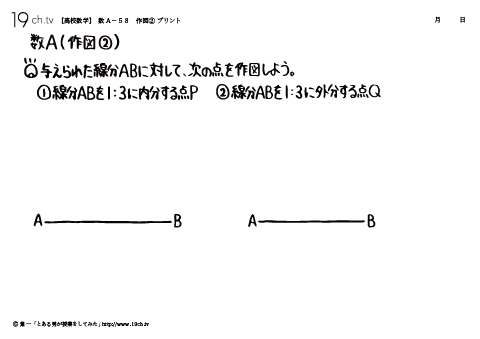
58		作図② 与えられた線分ABに対して、次の点を作図しよう。
59		作図③ 長さ1の線分ABと、長さa,bの2つの線分が与えられたとき、次の線分を作図しよう。

数A NO.60〜

NO.	イメージ	授業の内容	pdf
60		作図④ ①円0の外部の点Pから円Oに引いた接線を作図しよう。
61		作図⑤ ①1辺の長さを1とする正五角形の対角線の長さを求めよう。
62		直線と平面① 右の図の立方体において、次の2直線のなす角θを求めよう。ただし、0°≦θ≦90°とする。
63		直線と平面② 凸多面体の頂点の数をV、辺の数をe、面の数をfとすると、v-e+f=2が成り立つ。これをオイラーの多面体 定理という。
64		直線と平面③ 正八面体の体積を求めよう。
65		約数と倍数① ⑤12564は2.3.4.5.6.8.9のうち、どの数の倍数であるかを答えよう。
66		約数と倍数② ①196の正の約数をすべて求めよう。
67		約数と倍数③ 次の数が自然数になるような最小の自然数nを求めよう。
68		最大公約数・最小公倍数① ①168、196の最大公約数と最小公倍数を求めよう。
69		最大公約数・最小公倍数② ①積が6300であり、最小公倍数が420であるような2つの正の整数の最大公約数を求めよう。

数A NO.70〜

NO.	イメージ	授業の内容	pdf
70		最大公約数・最小公倍数③ ①aは自然数とする。a+5は4の倍数であり、a+3は6の倍数であるとき、a+9は12の倍数であることを証明しよう。
71		除法の性質① a、bは整数とする。aを7で割ると2余り、bを7で割ると5余る。このとき、次の数を7で割ったときの余りを求めよう。
72		除法の性質② ①80以下の自然数で、80と互いに素であるものの個数を求めよう。
73		除法の性質③ ①7^50を6で割った余りを求めよう。
74		合同式 合同式を用いて、次のものを求めよう。
75		ユークリッドの互除法 ユークリッドの互除法を用いて、次の数の最大公約数を求めよう。
76		１次不定方程式① 次の方程式の整数解をすべて求めよう。①5x+6y=0
77		１次不定方程式② ①113x+41y=3の整数解をすべて求めよう。
78		ｎ進法① 次の10進法で表された数を2進法で表そう。
79		ｎ進法② ①98を3進法で表そう。

数A NO.80〜

NO.	イメージ	授業の内容	pdf
80		ｎ進法③ ①11011(2)+111(2)
81		有限小数と循環小数 既約分数の形にしたとき、分母の素因数が2と5のみの分数は有限小数となる。
82		いろいろな方程式の整数解 ①xy−3x−2y+3=0を満たす整数x、yの組をすべて求めよう。

ページ上部へ戻る