数Ｉ

数Ｉの勉強動画ページ、無料プリント（PDF）のメニュー。
　高校数Ｉ 学習計画表 ? タイトルのみ表示

NO.	イメージ	授業の内容	pdf
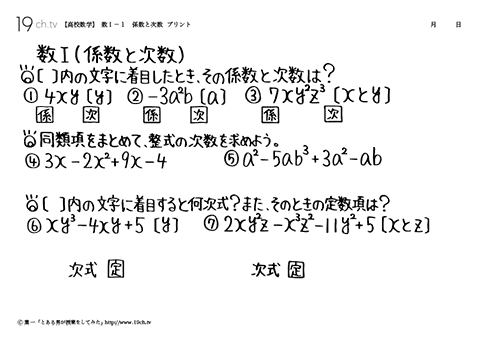
1		係数と次数 ［　］内の文字に着目したとき、その係数と次数は？同類項をまとめて、整式の次数を求めよう。
2		降べきの順 ［　］内の文字について降べきの順に整理しよう。
3		指数法則 am ×an =am+n
4		展開①・基本編 ※展開しよう。①（x−5y）2
5		展開②・練習編 ※展開しよう。①（x+4y）(3x－2y）
6		展開③・応用編 ※展開しよう。①（x+2y+3z）(x+2y−3z）
7		展開④・３次式の公式編 （a+b)3乗=（a+b）（a2− ab+b2）=
8		因数分解①・基本編 因数分解しよう。①3ax2−12a2x
9		因数分解②・たすき掛け編 ※因数分解しよう。①3ｘ2+5ｘ+2

数Ｉ NO.10〜

NO.	イメージ	授業の内容	pdf
10		因数分解③・応用編 ※因数分解しよう。①ｘy－ｘ+2y－2
11		因数分解④・３次式の公式編 ※a3乗+b3乗=(a+b)(a2－ab+b2) a3乗－b3乗=(a－b)(a2+ab+b2)
12		絶対値 ※a＞0のとき|a|=a、a=0のとき|a|=0a<0のとき|a|=－aとなる。
13		√シリーズ①・有理化編 ①2√5－5√2 / √5－√2
14		√シリーズ②・因数分解とのコラボ編 x=1/√5+2、y=1/√5−2のとき、次の式の値を求めよう。
15		√シリーズ③・応用編 1/2−√3の整数部分をa、少数部分をbとする。
16		√シリーズ④・二重根号編 2重根号をはずそう。 ① √（4+2√3）
17		１次不等式①・基本編 不等式を解こう。①4x−2＞3x+5
18		１次不等式②・練習編 ※不等式を解こう。①1/2x＞4/5x+3
19		１次不等式③・連立不等式編 ①{ 3x+8≧4x+2　{ 3x+4≧−2x

数Ｉ NO.20〜

NO.	イメージ	授業の内容	pdf
20		１次不等式 ④・応用編 ①不等式3x−a<2(5−x)を満たすxのうちで最大の整数が5であるとき、定数aの値の範囲は？
21		絶対値を含む方程式・不等式①・基本編 a＞0のとき、 |x|=aの解はx=± a
22		絶対値を含む方程式・不等式②・応用編 ① |x−3|=4x　② |x−4|≦3x
23		絶対値を含む方程式・不等式③・続・応用編 ①√x2+√(x2−4x+4）=4
24		集合① Uの部分集合A=｛1.2.4.8｝、B｛1.3.5.7.9｝について、次の集合を求めよう。
25		集合② Uの部分集合A=｛1.3.4.8｝、B=｛3.4.5.7.9｝、C=｛2.3.7.9｝について、次の集合を求めよう。
26		集合③ U=｛x|xは10以下の自然数｝の部分集合A、Bについて、
27		命題① a、b、cは実数、dは自然数とする。次の命題の真偽を調べ、偽のときは反例を1つ示そう。
28		命題② x、yは実数とする。次の□にあてはまるものを、下のA〜Dから選ぼう。
29		命題③ ①xy＞0は、x2+y2＞0が成立するための□

数Ｉ NO.30〜

NO.	イメージ	授業の内容	pdf
30		命題④ ※x、yは実数、m、nは自然数とする。次の条件の否定を書こう。
31		命題⑤ x、yは実数とする。次の命題の逆、裏、対偶を書き、それぞれの真意を調べよう。
32		命題⑥・背理法編 √2が無理数であることを用いて、5−√2が無理数であることを証明しよう。
33		命題⑦・続・背理法編 ※命題「nは整数とする。n2が3の倍数ならば、nは3の倍数である」は真である。
34		命題⑧ 等式を満たす有理数x、yの値を求めよう。
35		２次関数① f(x)=−2x+3について、次の値を求めよう。
36		２次関数②・値域編 関数の値域を求めよう。最大値、最小値があれば、それを求めよう。
37		２次関数③・軸と頂点編 次の2次関数の軸と頂点を求めよう。
38		２次関数④・平方完成編 2次式を平方完成しよう。
39		２次関数⑤・平方完成の練習編 ①y=ｘ2+2ｘ−1

数Ｉ NO.40〜

NO.	イメージ	授業の内容	pdf
40		２次関数⑥ 2次関数y=ax2+bx+cのグラフが右の図のようになるとき、次の値の符号を調べよう。
41		２次関数⑦・移動編 ①放物線y=−2x2−4x+1を軸方向に3、y軸方向に−1だけ平行移動して得られる放物線の方程式を求めよう。
42		２次関数の最大・最小① 2次関数に最大値、最小値があれば、それぞれ求めよう。
43		２次関数の最大・最小② ①y=2x2−3（−2≦x≦3）
44		２次関数の最大・最小③ ①y=3x2+6x+C（−2≦x≦1）の最大値が7となるような、 定数Cの値を求めよう。
45		２次関数の最大・最小④・動く軸編 関数y=x2−2ax+a（0≦x≦2）の最大値、最小値を、次の各場面について求めよう。
46		２次関数の最大・最小⑤・動く定義域編① a＞0とする。関数y=x2−2x−1（0≦x≦a）について。
47		２次関数の最大・最小⑥・動く定義域編② aは定数とする。関数y=x2−4x+5（a≦x≦a+1）について。
48		２次関数の最大・最小⑦ ①2x+y=1のとき、x2+y2の最小値を求めよう。
49		２次関数の決定① ①頂点が（1.−2）で点（2.−3）を通る。

数Ｉ NO.50〜

NO.	イメージ	授業の内容	pdf
50		２次関数の決定② 2次関数のグラフが、次の3点を通るとき、その2次関数を求めよう。
51		２次関数の決定③ 条件を満たす放物線の方程式を求めよう。
52		特殊な最大・最小① x≧0,　y≦0,　x−2y=3のとき、x2+y2の最大値、最小値を求めよう。
53		特殊な最大・最小② x、yを変数とするとき、x2−4xy+7y2−4y+3の最小値とそのときのx、yの値を求めよう。
54		２次方程式① ①x2−2x−3=0　②x2+7x=0
55		２次方程式② ① 2x2−5x+1=0
56		２次方程式③・判別式編 2次方程式の実数解の個数を求めよう。
57		２次方程式④ ①2次方程式 x2+4x+k=0が異なる2つの実数解をもつように、定数kの範囲を求めよう。
58		２次方程式⑤ 2つの2次方程式 x2−5x+3k=0、x2−3x+2k=0が共通な解をもつとき、定数kの値を定め、その共通解を求めよう。
59		２次関数と共有点① 2次関数のグラフとx軸の共通点の個数を求めよう。

数Ｉ NO.60〜

NO.	イメージ	授業の内容	pdf
60		２次関数と共有点② ① 3点（ −2 , 0 ）、( 3 , 0 ）、( 1 ,12）を通る2次関数を求めよう。
61		２次関数と共有点③ ①放物線 y=x2−3x+3と直線 y=2x−kが共有点をもたないように定数kの値の範囲を求めよう。
62		２次不等式① ① x2+5x+6＜0　② x2−4x+3＞0
63		２次不等式② ①x2−4x+2≦0　②−2x2−4x+5＜0
64		２次不等式③ ① x2−8x+16＞0
65		２次不等式④ ① 2次不等式　x2+ax+b＞0の解が　x ＜−2,　1＜x
66		２次不等式⑤ ①2次不等式 x2−2ax+a+b＞0の解がすべての実数であるとき、aの値の範囲は？
67		２次不等式⑥ 0≦x≦2の範囲において、常にx2−2ax+3a＞0が成り立つように、定数aの値の範囲を求めよう。
68		２次不等式⑦・連立不等式編 ①　x2−x−12≦0　 　　x2−3x+2＞0
69		２次不等式⑧ ①　x2−x−12≦0　 　　x2−3x+2＞0

数Ｉ NO.70〜

NO.	イメージ	授業の内容	pdf
70		２次不等式⑨ 2つの2次方程式 x2−x+a=0、x2+2ax−3a+4=0について、次の条件を満たす定数aの値の範囲をもとめよう。
71		２次関数と共有点④ 周囲の長さが20cmの長方形の面積を9㎠以上、21㎠以下にするには、短い方の辺の長さをどのような範囲にとればよいか求めよう。
72		２次関数と共有点⑤ 2次方程式 2x2−5x+a=0の1つの解が0と1の間にあり、他の解が2と3の間にあるように、定数aの値の範囲を定めよう。
73		特殊な最大・最小③ x、yがx2+y2=16を満たすとき、6x+y2の最大値と最小値を求めよう。
74		絶対値を含む関数のグラフ① 次の関数のグラフを書き、その値域を求めよう。
75		絶対値を含む関数のグラフ② y=｜2x2−4x−6｜のグラフを書こう。
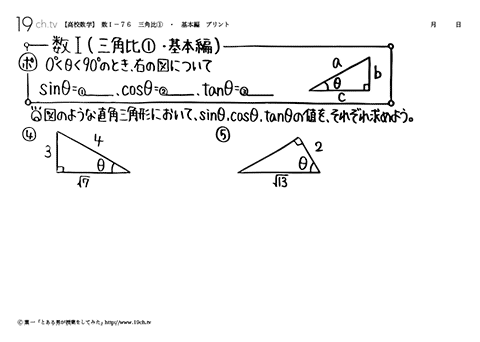
76		三角比①・基本編 0°＜θ＜90°のとき、右の図について
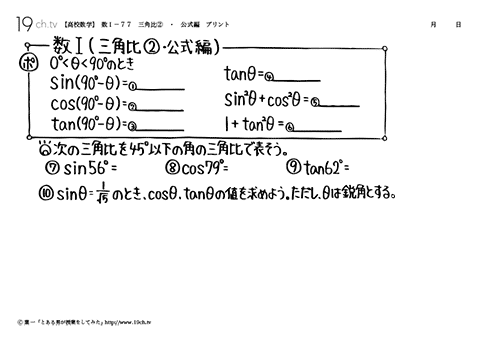
77		三角比②・公式編 次の三角比を45°以下の角の三角比で表そう。
78		三角比③ ①（sinθ+cosθ)2+（sinθ−cosθ)2
79		三角比④・暗記編 θ　0° 30° 45°60° 90°120° 135° 150° 180°

数Ｉ NO.80〜

NO.	イメージ	授業の内容	pdf
80		三角比⑤ sin105°−cos150°+sin120°+cos165°の値は？
81		三角比⑥ 0°≦θ≦180°のとき、次の等式を満たすθを求めよう。
82		三角比⑦ 次の式のとりうる値の範囲を求めよう。
83		三角比⑧ 0°≦θ≦180°のとき、sinθ+cosθ=1/2のとき、 次の式の値を求めよう。
84		三角比⑨ 0°≦θ≦180°とする。次の不等式を満たすθの範囲を求めよう。
85		三角比⑩ 0°≦θ≦180°であるとき、y=cos2θ−2sinθ−1の最大値と最小値を求め、 そのときのθも求めよう。
86		正弦定理 △ABCの外接円の半径をRとすると① a/sinA = ②b/sinB= ③c/sinC=2R
87		余弦定理 △ABCについて ① a2=b2+c2−2bc cosA
88		正弦定理と余弦定理① △ABCにおいて、次のものを求めよう。①B=60°、c=75°、b=2√6のとき
89		正弦定理と余弦定理② △ABCにおいて、a=2、b=√6、A=45°のとき、残りの辺の長さと角の大きさを求めよう。

数Ｉ NO.90〜

NO.	イメージ	授業の内容	pdf
90		正弦定理と余弦定理③ △ABCにおいて、次が成り立つとき、この三角形の最も大きい角の余弦の値を求めよう。
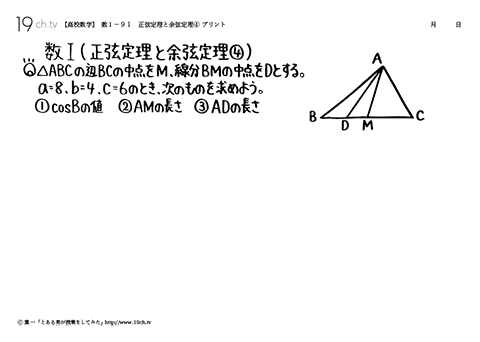
91		正弦定理と余弦定理④ △ABCの辺BCの中点をM、線分BMの中点をDとする。a=8、b=4、c=6のとき、次のものを求めよう。
92		三角形となる条件 3辺の長さが、5、3、xである三角形が鈍角三角形となるように、xの範囲を定めよう。
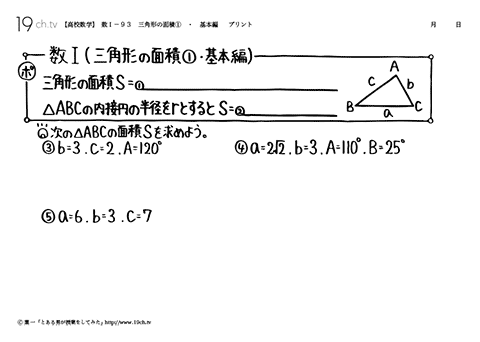
93		三角形の面積①・基本編 三角形の面積S=1/2bc sinA（1/2casinB=1/2ab sinC) △ABCの内接円の半径をrとするとS=1/2r（a+b+c）
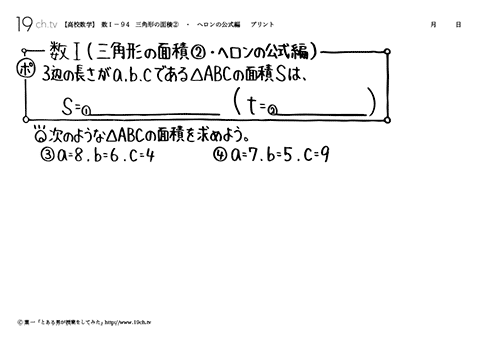
94		三角形の面積②・ヘロンの公式編 3辺の長さがa、b、cである△ABCの面積Sは、 S=√t(t−a) (t−b) (t−c) ｛t=（a+b+c）/2｝
95		多角形の面積 次のような図形の面積Sを求めよう。 ①AB=5、BC=8、CD=4、∠B=∠C=60°の四角形ABCD
96		円に内接する四角形 円に内接する四角形ABCDがあり、AB=3、BC=1、CD=3、DA=4である。
97		内接円と外接円の半径 外接円の半径Rは？内接円の半径rは？
98		三角形の内角の二等分線 二等分線が辺BCと交わる点をDとするとき、線分ADの長さを求めよう。
99		正四面体の切り口 1辺の長さが6の正四面体OABC。①LMの長さは？
100		立体に内接する球 右図のように、高さ4、底面の半径√2の円錐が球Oと側面で接し、底面の中心Mでも接している。

ページ上部へ戻る