数Ⅱ

数Ⅱの勉強動画ページ、無料プリント（PDF）のメニュー。
　高校数Ⅱ 学習計画表 ?

数Ⅱ NO.100〜

タイトルのみ表示

NO.	イメージ	授業の内容	pdf
100		三角関数を含む方程式・不等式② 0≦θ≦2πのとき、次の不等式を解こう。
101		三角関数を含む方程式・不等式③ 0≦θ≦2πのとき、次の方程式を解こう。
102		三角関数を含む方程式・不等式④ 0≦θ≦2πのとき、次の不等式を解こう。
103		三角関数を含む方程式・不等式⑤ 0≦θ≦2πのとき、次の方程式を解こう。
104		三角関数を含む方程式・不等式⑥ 0≦θ≦2πのとき、次の不等式を解こう。
105		三角関数を含む関数の最大・最小① 次の関数の最大値と最小値、および、そのときのθの値を求めよう。
106		三角関数を含む関数の最大・最小② 次の関数の最大値と最小値、および、そのときのθの値を求めよう。
107		加法定理① sin(α+β）=sinαcosβ+cosαsinβ
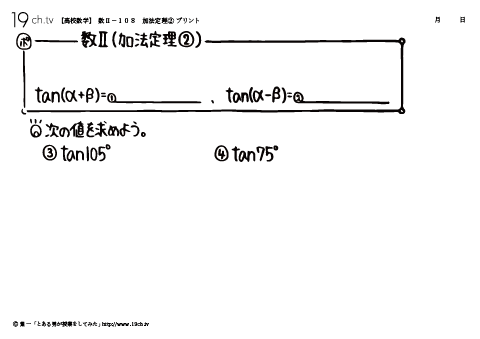
108		加法定理② tan(α+β）=(tanα+ tanβ)/（1−tanα tanβ）
109		2直線のなす角 次の2直線のなす角θを求めよう。

数Ⅱ NO.110〜

NO.	イメージ	授業の内容	pdf
110		点の回転 ①点P（3,4）を、原点Oを中心として、2/3πだけ回転させた点Qの座標を求めよう。
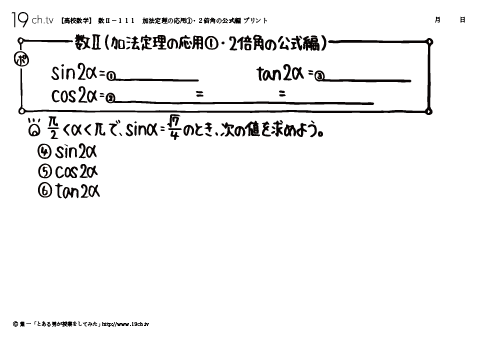
111		加法定理の応用①・２倍角の公式編 π/2＜α＜πで、sinα=√7/4のとき、次の値を求めよう。
112		加法定理の応用②・３倍角の公式編 ①sin3α=3sinα−4sin3αを証明しよう。
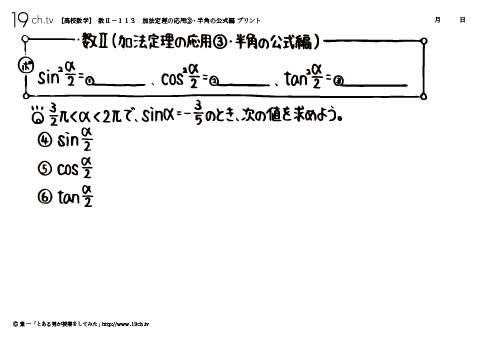
113		加法定理の応用③・半角の公式編 ○3/2π＜α＜2πで、sinα=−3/5のとき、次の値を求めよう。
114		三角関数を含む方程式・不等式⑦ 0≦x＜2πのとき、次の方程式を解こう。
115		三角関数を含む方程式・不等式⑧ 0≦x＜2πのとき、次の不等式を解こう。
116		和と積の公式①・積→和(差)編 次の値を求めよう。⑤sin75°cos15°
117		和と積の公式②・和(差)→積編 次の値を求めよう。⑤sin105°+sin15°
118		三角関数の合成① 次の式をrsin(θ+α)の形に変形しよう。
119		三角関数の合成② 0≦x＜2πのとき、次の方程式を解こう。

数Ⅱ NO.120〜

NO.	イメージ	授業の内容	pdf
120		三角関数の合成③ 0≦x＜2πのとき、次の不等式を解こう。
121		三角関数の合成④ ① 0≦θ＜2πのとき、関数y=−sinθ+ √3cosθの最大値と最小値、およびそのときのθの値を求めよう。
122		三角関数の合成⑤ ①関数y=2sinxcosx+sinx+cosx+1の最大値と最小値を求めよう。
123		指数の拡張① 次の値を求めよう。②３-2
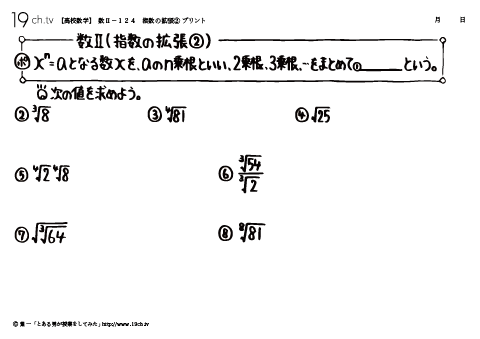
124		指数の拡張② 2乗根、3乗根、・・・をまとめて累乗根という。
125		指数の拡張③ ①（32)-3×33÷9-2
126		指数の拡張④ ①（a ^1/3+b^1/3）(a ^2/3−a ^1/3b^1/3）+b^2/3）を計算しよう。
127		指数関数①・グラフ編 a＞0、 a≠1とするとき、y=a^xはxの関数で、関数y=a^xをaを底とするxの指数関数という。
128		指数関数②・性質編 次の数の大小を不等号を用いて表そう。
129		指数関数③・方程式編 次の方程式を解こう。②（1/3)^x=9

数Ⅱ NO.130〜

NO.	イメージ	授業の内容	pdf
130		指数関数④・不等式編 ①2 ^x−32＞0
131		対数とその性質① aを底とするMの対数といい、logaMと書く。 また、Mをこの対数の真数という。
132		対数とその性質② 次の値を求めよう。①log216
133		対数とその性質③ 底の変換公式を用いて、次の値を求めよう。
134		対数とその性質④ ①log23=a、log37=bとするとき、log4256をa,bで表そう。 ほか。
135		対数関数①・グラフ編 a＞0、 a≠1とするとき、関数y=logaxを、aを底とするxの 対数関数という。
136		対数関数②・性質編 次の数の大小を不等号を用いて表そう。
137		対数関数③・方程式編 次の方程式を解こう。① log3x=2
138		対数関数④・不等式編 次の不等式を解こう。① log3x＜3/2
139		指数関数・対数関数の最大値・最小値① ①　関数y=2^2x−4・2^x+1の最小値を求めよう。

数Ⅱ NO.140〜

NO.	イメージ	授業の内容	pdf
140		指数関数・対数関数の最大値・最小値② ①関数y=4^x−2^x+1の最小値を求めよう。
141		常用対数① 10を底とする対数を常用対数という。
142		常用対数② ①2^50は何桁の整数か求めよう。
143		常用対数③ ①1.2^n＜100を満たす最大の整数nを求めよう。
144		微分係数と導関数① 次の関数の与えられた範囲における平均変化率を求めよう。
145		微分係数と導関数② 次の関数を微分しよう。
146		微分係数と導関数③ 次の条件を満たす3次関数f(x)を求めよう。
147		接線① 次の曲線上における、曲線の接線の方程式を求めよう。
148		接線② ①曲線y=x3−5x上の点（1,−4）における接線に 垂直な直線な方程式を求めよう。
149		接線③ ①2曲線y=x2+1、y=−2x2+4x−3の共通接線の方程式を求めよう。

数Ⅱ NO.150〜

NO.	イメージ	授業の内容	pdf
150		関数の値の変化 次の関数の増減を調べよう。
151		関数の極値① 次の関数の極値を求めて、そのグラフを書こう。
152		関数の極値② 次の関数の極値を求めて、そのグラフを書こう。
153		関数の極値③ 次の関数の極値を求めて、そのグラフを書こう。
154		関数の極値④ ① 関数f(x)=x3−4x2+axがx=2で極小値をとるとき、aの値を求めよう。
155		関数の極値⑤ ① 関数f(x)=x3+ax2+3xが常に単調に増加する。
156		関数の最大値・最小値① 次の関数の最大値と最小値を求めよう。
157		関数の最大値・最小値② x+3y=9、x≧0、y≧0のとき、次の問いに答えよう。
158		関数の最大値・最小値③ 0≦x＜2πのとき、関数y=cos2x−2cos3xの最大値と最小値、およびそのときのxの値を求めよう。
159		関数の最大値・最小値④ a＞0とする。関数f(x)=ax3+3ax2+b（−1≦x≦2）の最大値が10、最小値が−8であるとき、定数a、bの値を求めよう。

数Ⅱ NO.160〜

NO.	イメージ	授業の内容	pdf
160		関数の最大値・最小値⑤ f(x)=x3−3ax2+5a3の0≦x≦3における最小値を求めよう。ただし、a＞0とする。
161		関数の最大値・最小値⑥ ① 関数f(x)=x3−3x2+2（0≦x≦a）の最大値と最小値、および、そのときのxの値を求めよう。
162		関数のグラフと方程式・不等式① 次の方程式の異なる実数解の個数を求めよう。
163		関数のグラフと方程式・不等式② 3次方程式x3+3x2−a=0について。次の問いに答えよう。
164		関数のグラフと方程式・不等式③ 方程式x3−6x+a=0が異なる2個の負の解と1個の正の解をもつように、定数aの値の範囲を定めよう。
165		関数のグラフと方程式・不等式④ ①　x＞0とする。不等式x3−6x2≧−9xを証明しよう。
166		不定積分① 次の不定積分を求めよう。
167		不定積分② ①条件f′(x)=6x2−2x−3、F(2)=0を満たす関数F(x)を求めよう。
168		定積分① 次の定積分を求めよう。
169		定積分② 次の定積分を求めよう。

数Ⅱ NO.170〜

NO.	イメージ	授業の内容	pdf
170		定積分で表された関数① ①∫x2（3t2−4t−1）dtをxの式で表そう。
171		定積分で表された関数② ① 等式f(x)=3x2−2∫1-1 f(t)dtを満たす関数 f(x)を求めよう。
172		定積分と面積① 次の曲線や直線で囲まれた図形の面積Sを求めよう。
173		定積分と面積② 次の曲線や直線で囲まれた図形の面積Sを求めよう。
174		定積分と面積③ ①曲線y=x3−6x2+8xとx軸で囲まれた2つの部分の面積の和Sを求めよう。
175		定積分と面積④ 次の定積分を求めよう。
176		定積分と面積⑤ ①点Aにおける放物線の接線の方程式を求めよう。
177		定積分と面積⑥ 接線で囲まれた図形の面積Sを求めよう。
178		定積分と面積⑦ ①放物線　y=x2+2xとx軸で囲まれた部分の面積が、直線y=axによって2等分されるとき、定数aの値を求めよう。

ページ上部へ戻る