数Ⅱ

数Ⅱの勉強動画ページ、無料プリント（PDF）のメニュー。
　高校数Ⅱ 学習計画表 ? タイトルのみ表示

NO.	イメージ	授業の内容	pdf
1		３次式の展開と因数分解 展開（⑤・⑥）因数分解（⑦・⑧）しよう。
2		パスカルの三角形 パスカルの三角形を利用して、展開しよう。
3		二項定理① 二項定理を利用して展開しよう。
4		二項定理② 展開式における［　］に指定された項の係数は？
5		整式の割り算① 次のA、Bについて、AをBで割った商と余りを求めよう。
6		整式の割り算② 次のxについての整式A、Bにおいて、AをBで割った商と余りを求めよう。
7		整式の割り算③ ①x2−2x−1で割ると、商が2x−3、余りが−2xになる整式は？
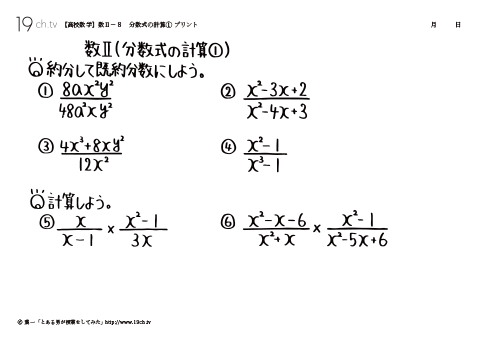
8		分数式の計算① 約分して既約分数にしよう。
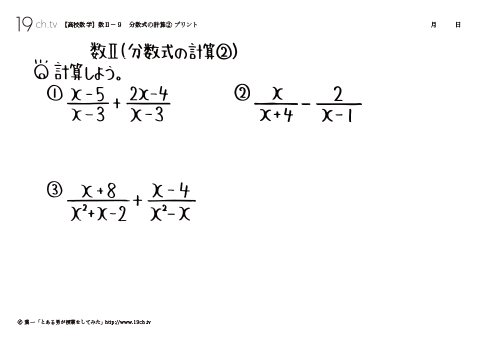
9		分数式の計算② ①(x−5）/(x−3）+（2x−4) / (x−3）

数Ⅱ NO.10〜

NO.	イメージ	授業の内容	pdf
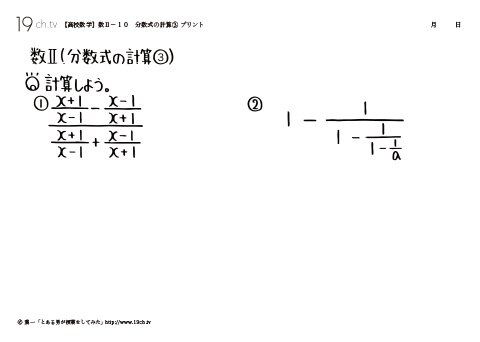
10		分数式の計算③ ①｛（x+1）/（x−1)−（x−1)/（x+1）｝/｛（x+1）/（x−1)+（x−1)/（x+1）｝
11		分数式の計算④ ①1/（a−b) (b−c)+2/ (b−c)(c−a)+3/(c−a)（a−b)
12		恒等式① 等式がxについての恒等式となるように、定数a、b、cの値を定めよう。
13		恒等式② 次の等式がxについての恒等式となるように、定数a、 b、 c の値を定めよう。
14		恒等式③ 等式がx、yの恒等式となるように、定数a、 b、 c の値を定めよう。
15		恒等式④ ① x+y=1を満たすx、yについて、常にax2+by+cx=2が成り立つとき、 定数a、b、cの値を求めよう。
16		等式の証明① ①(a＋2b)2+(a－b)2=2(a2＋4b)を証明しよう。
17		等式の証明② ①a/b=c/dのとき、(a2－b2)/(a2＋b2)=(c2－d2)/(c2＋d2)が成り立つことを証明しよう。
18		等式の証明③ ①x+y+z=3、xyz=3(xy+yz+zx)のとき、x、y、zのうち少なくとも 1つは3に等しいことを証明しよう。
19		不等式の証明① ① x2+4x+4 ≧ −y2+2y−1

数Ⅱ NO.20〜

NO.	イメージ	授業の内容	pdf
20		不等式の証明② a＞0、b＞0のとき、√（4a+9b）＜2√a+3√bを証明しよう。
21		不等式の証明③ a＞0、b＞0のとき、次の不等式を証明しよう。また、等号が成り立つ場合を調べよう。
22		不等式の証明④ 0＜a＜b、a＋b=1のとき、b、2ab、a2+b2を小さい方から順に並べよう。
23		複素数① 複素数の実部と虚部を書こう。
24		複素数② ①（5+2i）+（−2−i）
25		複素数③ 複素数と共役な複素数を書こう。
26		複素数④ 次の数の平方根を書こう。①5
27		複素数⑤ α=（3+i)/（2+i)+（x−i)/（2−i)がつぎのようなとき、実数xの値を求めよう。
28		2次方程式の解と判別式① 次の方程式を解こう。①x2=9
29		2次方程式の解と判別式② 次の2次方程式を解こう。①−2x2−7=−6x

数Ⅱ NO.30〜

NO.	イメージ	授業の内容	pdf
30		2次方程式の解と判別式③ 2次方程式の解の種類を判別しよう。
31		2次方程式の解と判別式④ ①x2−(a−8)x+a=0
32		2次方程式の解と判別式⑤ aは定数とするとき、方程式ax2+6x+a−8=0の解の種類を判別しよう
33		2次方程式の解と判別式⑥ ①2次方程式4x23（k−1）x+1=0が重解をもつとき、定数kの値とその解を求めよう。
34		解と係数の関係① 次の2次方程式の2つの解の和と積を求めよう。
35		解と係数の関係② 2次方程式x2+3x+1=0の2つの解をα、βとすると、次の式の値を求めよう。
36		解と係数の関係③ 次の2次式を、複素数の範囲で因数分解しよう。
37		解と係数の関係④ 次の2数を解とする2次方程式を1つ作ろう。ただし、係数は整数とする。
38		解と係数の関係⑤ 2次方程式x2+3x−2=0の2つの解をα、βのとき、次の2数を解とする2次方程式を1つ作ろう。ただし、係数は整数とする。
39		解と係数の関係⑥ 2次方程式x2−mx+2m+5=0が次のような異なる2つの解を もつように、定数mの値の範囲を定めよう。

数Ⅱ NO.40〜

NO.	イメージ	授業の内容	pdf
40		解と係数の関係⑦ ①2次方程式x2−(m−1)x+m+6=0がともに2以上である2つの解を もつとき、定数mの値の範囲を定めよう。
41		解と係数の関係⑧ ①x2−2kx+4k+5が1次式の2乗となるように、 定数kの値を定めよう。
42		剰余の定理と因数定理① 次の整式［　］内の整式で割ったときの余りを求めよう。
43		剰余の定理と因数定理② 次の式を因数分解しよう。
44		剰余の定理と因数定理③ ① x2+ax+bが、x+1で割ると1余り、x−1で割ると3余るとき定数a,、bの値を求めよう。
45		剰余の定理と因数定理④・組立除法編 組立除法を用いて、次の計算をして、商と余りを求めよう。
46		高次方程式① 次の方程式を解こう。①（x−2）(2x+1)=0
47		高次方程式② 次の方程式を解こう。① x3−7x+6=0
48		高次方程式③ 1の3乗根の1つである（−1+√3i)/2をwとするとき、次の式の値を求めよう。
49		高次方程式④ 3次方程式 x3+ax2+bx+10=0 の1つの解が2−iであるとき、実数a、bの値と他の解を求めよう。

数Ⅱ NO.50〜

NO.	イメージ	授業の内容	pdf
50		高次方程式⑤ 3次方程式 x3+2x2+4x+3=0 の3つの解をα、β、rとするとき、次の式の値を求めよう。
51		点と直線① 次の2点間の距離を求めよう。
52		点と直線② 次の2点間の距離を求めよう。
53		点と直線③ 2点A（−3、4）、B（1、2）を結ぶ線分ABについて、次の点の座標を求めよう。
54		点と直線④ ①点A（−2、3）に関して、点B(4、1）と対称な点C
55		点と直線⑤ ①3点A（4、5）B（6、７）C（7、3）を頂点とする平行四辺形の残りの頂点Dの座標を求めよう。
56		直線の方程式① 次の直線の方程式を求めよう。
57		直線の方程式② 次の直線は、y= −3x+2に平行、垂直のどちらかを書こう。
58		直線の方程式③ 次の直線に関して、点（3、1）と対称な点を求めよう。
59		直線の方程式④・点と直線の距離編 次の点と直線の距離を求めよう。

数Ⅱ NO.60〜

NO.	イメージ	授業の内容	pdf
60		直線の方程式⑤ ①3直線x+2y=0、x=y−1、y=−2x+2で作られる三角形の面積を求めよう。
61		直線の方程式⑥ ①x+y=0、x+3y−2=0、ax−2y+4=0が三角形を作らないとき、 定数aの値を求めよう。
62		円と直線① 次の円の方程式を求めよう。①中心が（1、2）、半径が3
63		円と直線② 次の方程式はどのような図形を表しているか書こう。
64		円と直線③ ①3点A、B、Cを通る円の方程式を求めよう。
65		円と直線の共有点① 次の円と直線の共有点の座標を求めよう。
66		円と直線の共有点② 次の円と直線の共有点の個数を求めよう。
67		円と直線の共有点③ ① 円x2+y2=1と直線y=x+kが共通点をもつとき、定数kの値の範囲を求めよう。
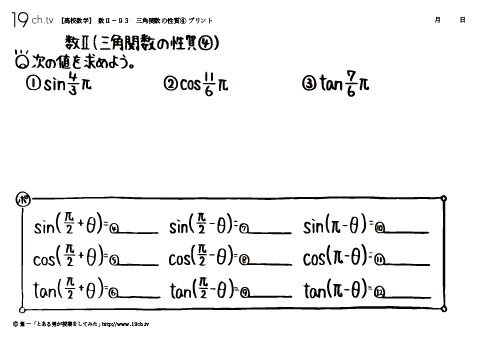
68		円の接線の方程式① 円上の点Pにおける接線の方程式を求めよう。
69		円の接線の方程式② ①円x2+y2+4x−6y−12=0上の点（1、7）における接線の方程式を求めよう。

数Ⅱ NO.70〜

NO.	イメージ	授業の内容	pdf
70		円の接線の方程式③ ①2円x2+y2=1、（x−3)2+y2=4の両方に接する接線の方程式を求めよう。
71		２つの円① 次の2つの円の位置関係を（2点で交わる・外接する・内接する・共通点がない）から選ぼう。
72		２つの円② ①中心が点（5、12）で、円x2+y2=9に外接する円を求めよう。
73		２つの円③ ①x2+y2=10、x2+y2−2x−y−5=0
74		２つの円④ ①円x2+y2=50と直線3x+y=20の2つの交差点と 点（10、0）を通る直線の方程式を求めよう。
75		軌跡と方程式① 次の条件を満たす点Pの軌跡を求めよう。
76		軌跡と方程式② 次の条件を満たす点Pの軌跡を求めよう。
77		軌跡と方程式③ ①点Qが直線2x−y+5=0上を動くとき、原点Oと点Qを結ぶ線分OQを 2：1に内分する点Pの軌跡を求めよう。
78		不等式の表す領域① 次の不等式の表す領域を図示しよう。
79		不等式の表す領域② ①x2+y2＜4

数Ⅱ NO.80〜

NO.	イメージ	授業の内容	pdf
80		不等式の表す領域③ 次の不等式の表す領域を図示しよう。
81		不等式の表す領域④ 次の不等式の表す領域を図示しよう。
82		不等式の表す領域⑤ 次の不等式の表す領域を図示しよう。
83		領域と最大・最小① ①x、yが4つの不等式x≧0、y≧0、x+3y≦6、2x+y≦7を満たすとき、x+yの最大値および最小値をもとめよう。
84		領域と最大・最小② ①x、yが3つの不等式x+2y−4≧0、3x+y−12≦0、x−3y+6≧0を満たすとき、4x+yの最大値および最小値を求めよう。
85		領域と最大・最小③ ①x、yが3つの不等式x−3y≧−6、x+2y≧4、3x+y≦12を満たすとき、x2+y2の最大値および最小値を求めよう。
86		絶対値を含む領域 次の不等式の表す領域を図示しよう。
87		一般角と弧度法 次の角の動径を図示しよう。
88		扇形の弧の長さと面積 扇形の弧の長さと面積を求めよう。
89		一般角の三角関数 座標平面上で、x軸の正の部分を始線にとり、一般角θの動径と、原点を中心とする半径rの円との交点Pの座標を（x、y）とすると...

数Ⅱ NO.90〜

NO.	イメージ	授業の内容	pdf
90		三角関数の性質① sinθ、cosθ、tanθのうち、1つが次のように与えられたとき、他の2つの値を求めよう。
91		三角関数の性質② sinθcosθ=1/2（π＜θ＜3/2π）のとき、次の式の値を求めよう。
92		三角関数の性質③ 次の値を求めよう。①sin7/3π
93		三角関数の性質④ 次の値を求めよう。①sin4/3π
94		三角関数の性質⑤ ① sin（π/2+θ）+ sin（π/2−θ）+cos（−θ）
95		三角関数のグラフ① 次の関数のグラフと周期を書こう。
96		三角関数のグラフ② 次の関数のグラフと周期を書こう。
97		三角関数のグラフ③ 次の関数のグラフと周期を書こう。
98		三角関数のグラフ④ 次の関数のグラフと周期を書こう。
99		三角関数を含む方程式・不等式① 0≦θ≦2πのとき、次の方程式を解こう。

続きはこちら






ページ上部へ戻る