テスト対策・中2数学

テスト対策・中2の勉強動画ページ、無料プリント（PDF）のメニュー。
　テスト対策・中2 学習計画表 ?

タイトルのみ表示

NO.	イメージ	授業の内容	pdf
1		中2・1章-1 ①(−3x)²×2ｙ÷(−3xy） ②3/4x²y÷x^3y×(−2xy)²
2		中2・1章- 2 ①x=2/5、y=−1/3のとき、6(4x−5y)−4(x−3y)の値を求めなさい。
3		中2・1章- 3 ［］内の文字について解きなさい。①2a-3b+4c=0［a］
4		中2・1章- 4 次の□にあてはまる式を書き入れなさい。□×5xy=−20x²y
5		中2・２章－１ ①｛0.3x+0.7y=5　0.9x+1/10y=−1
6		中2・２章－2 ①連立方程式｛ax+by=−11　bxーay=13の解がx=3、y=-1であるとき a、bの値を求めなさい。
7		中2・２章－3 ①x、yについての3つの二元一次方程式｛3x+2y=8　4x-5y=3　5x−ay=4のすべてにあてはまる解があるとき、その解とaの値を求めなさい。
8		中2・２章－4 ①ある工場で、先月は、製品AとBをあわせて1000個つくりました。今月は、先月とくらべて、Aを10％多く、Bを20％少なくつくったところ、あわせて95個少なくなりました。先月つくった製品A、Bの個数を、それぞれ求めなさい。
9		中2・３章－１ ①一次関数 y=−2/3x+1/5について、xの増加量が10のとき、yの増加量を求めなさい。

NO.10〜

NO.	イメージ	授業の内容	pdf
10		中2・３章－２次の一次関数の式を求めなさい。①2点（-2、5）、（1、-4）を通る直線
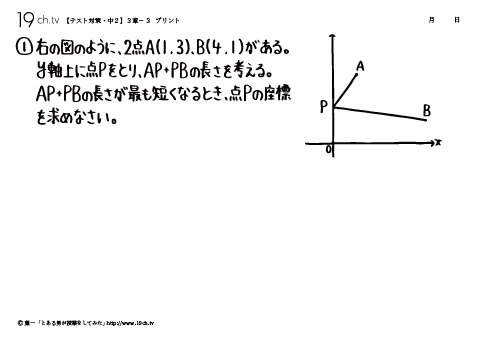
11		中2・３章－3 2点A（1、3）、B(4、1）がある。y軸上に点Pをとり、AP+PBの長さを考える。
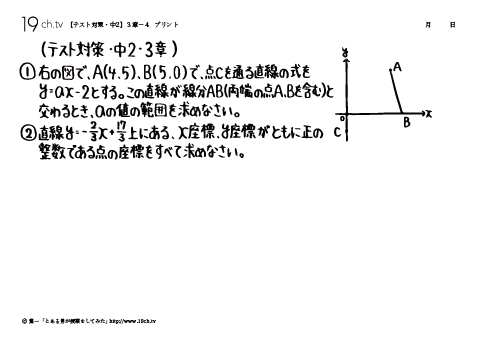
12		中2・３章－４ ②直線y=−2/3x+17/3上にある、x座標、y座標がともに正の整数である点の座標をすべて求めなさい。
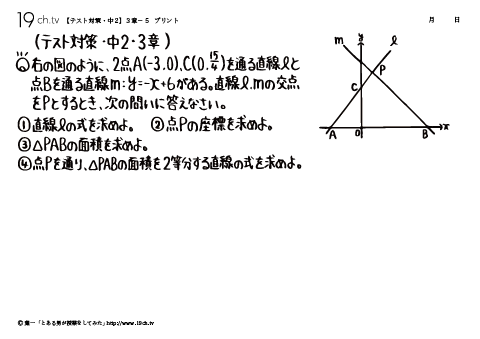
13		中2・３章－５右の図のように、2点A（-3、0）、C(0、15/4）を通る直線lと点Bを通る直線m：y=ーx+6がある。直線l、mの交点をPとするとき、次の問いに答えなさい。
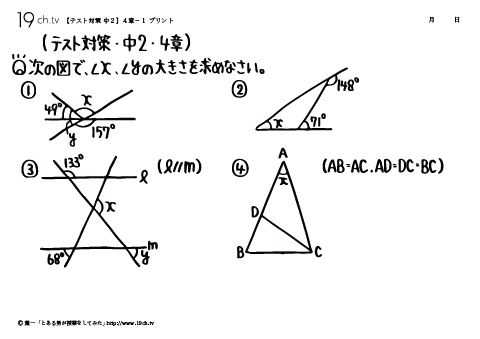
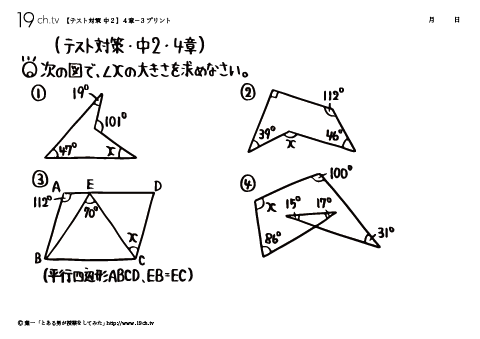
14		中2・4章- 1 次の図で、∠x、∠yの大きさを求めなさい。
15		中2・4章- 2 右の図形について□にあてはまる式や数を書きなさい。
16		中2・4章- 3 次の図で、∠xの大きさを求めなさい。
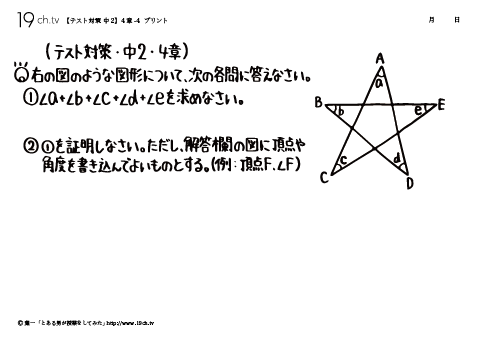
17		中2・4章- 4 ①を証明しなさい。ただし、解答欄の図に頂点や角度を書き込んでよいものとする。
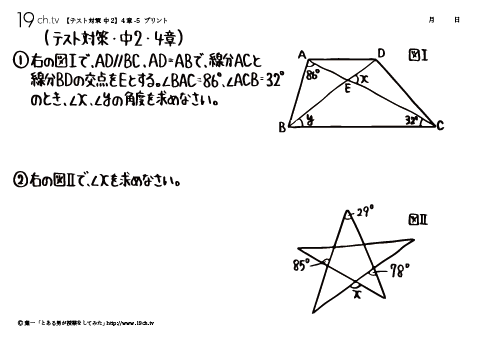
18		中2・4章- 5 ∠BAC=86°、∠ACB=32°のとき、∠x、∠yの角度を求めなさい。
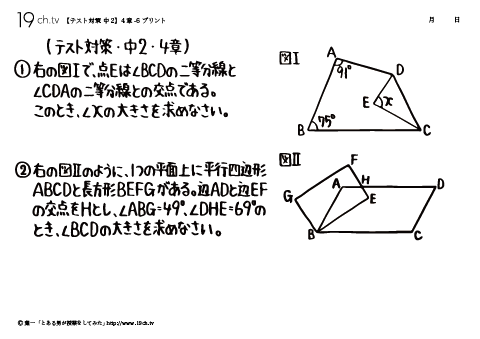
19		中2・4章- 6 ①右の図Ⅰで、点Eは∠BCDの二等分線と∠CDAの二等分線との交点である。

NO.20〜

NO.	イメージ	授業の内容	pdf
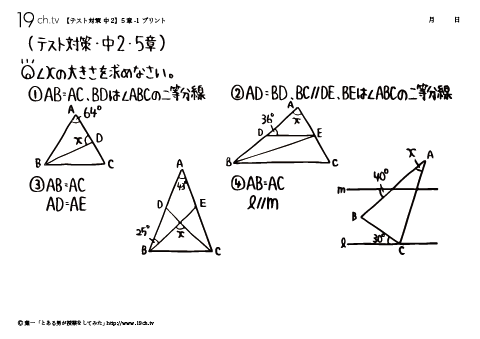
20		中2・5章- 1 二等辺三角形①AB=AC、BDは∠ABCの二等分線 ②AD=BD、BC//DE、BEは∠ABCの二等分線
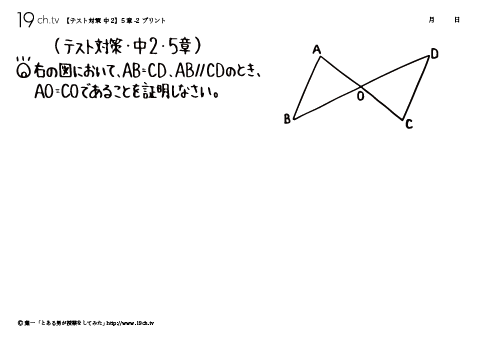
21		中2・5章- 2 右の図において、AB=CD、AB//CDのとき、AO=COであることを証明しなさい。
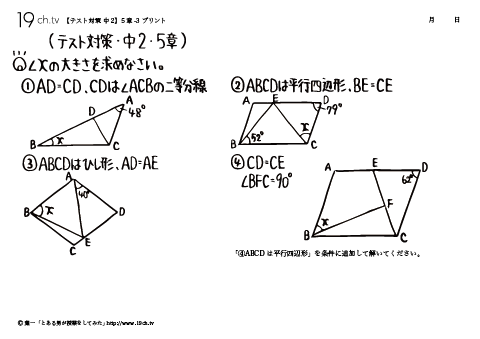
22		中2・5章- 3 ○∠xの大きさを求めなさい。①AD=CD、CDは∠ACBの二等分線
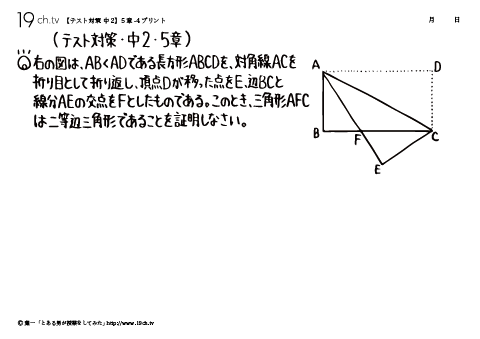
23		中2・5章- 4 三角形AFCは二等辺三角形であることを証明しなさい。
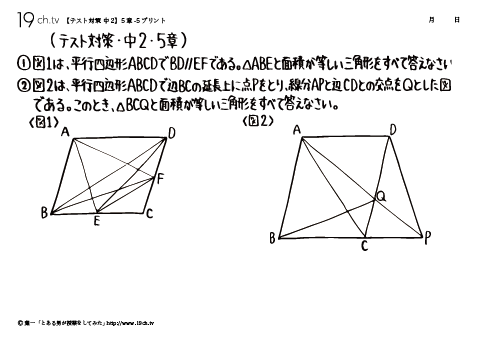
24		中2・5章- 5 平行四辺形ABCDでBD//EFである。△ABEと面積が等しい三角形をすべて答えなさい。
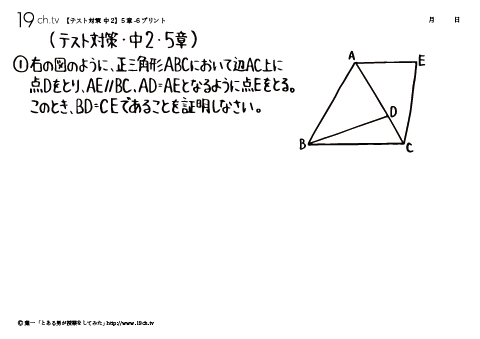
25		中2・5章- 6 正三角形ABCDにおいて辺AC上に点Dをとり、AE//BC、AD=AEとなるように点Eをとる。このとき、BD=CEであることを証明しなさい。
26		中2・6章-1 ①1,1,1,2,3の5枚のカードから2枚取り出して2桁の整数をつくるとき、奇数となるのは全部で何通りか求めなさい。
27		中2・6章-2 ①A,B,C,D,Eの5人が1列に並ぶ。AとBが端になるようにするとき、並び方は何通りあるか求めなさい。
28		中2・6章-3 ①大小2個のさいころを同時に投げるとき、出る目の数の積が3の倍数になる確率。
29		中2・6章-4 ①当たりが3本は入った5本のくじがある。このくじをA,Bの2人がこの順に1本ずつ引くとき 2人とも当たりを引く確率を求めなさい。
30		中2・6章-5 ①赤玉2個と白玉4個が入っている袋から、同時に2個取り出すとき、少なくとも1個が赤玉である確率を求めよ。

ページ上部へ戻る