高校数学（数B）

高校 数Bの勉強動画ページ、無料プリント（PDF）のメニュー。
　高校数B 学習計画表 ? タイトルのみ表示

NO.	イメージ	授業の内容	pdf
1		有向線分とベクトル 向きを指定した線分を有向線分といい、Aを始点、Bを終点という。
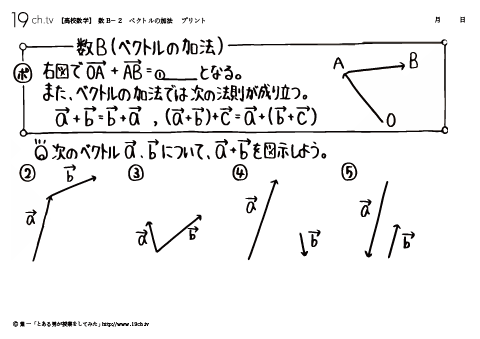
2		ベクトルの加法 右図でOA→+AB→ =OB→となる。また、ベクトルの加法では次の法則が成り立つ。
3		ベクトルの減法 a→と大きさが等しく、向きが反対であるベクトルを－a→で表し、これをa→の逆ベクトルという。
4		ベクトルの式の計算① 次の式を簡単にしよう。①（3a→−2b→）−（a→−5b→）
5		ベクトルの式の計算② 次の等式を満たすx→ 、y→をa→、b→で表そう。
6		ベクトルの平行 ①e→を単位ベクトルとするとき、e→と平行で、大きさが5のベクトルを求めよう。
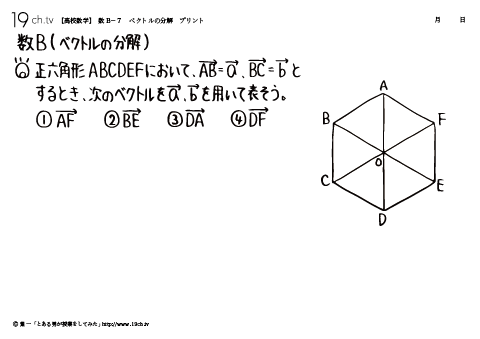
7		ベクトルの分解 正六角形ABCDEFにおいて、AB→=a→、BC=b→とするとき、次のベクトルをa→、b→を用いて表そう。
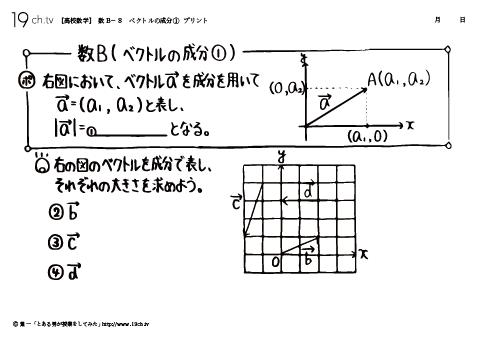
8		ベクトルの成分① 右の図のベクトルを成分で表し、それぞれの大きさを求めよう。
9		ベクトルの成分② ①a→=（2,1）、b→=（−2,3）であるとき、3a→−b→を成分で表そう。

数B NO.10〜

NO.	イメージ	授業の内容	pdf
10		ベクトルの成分③ 4点0（0,0）、A（3,0）、B（−1,2）C（−1,−4）について、次のベクトルを成分で表し、それぞれの大きさを求めよう。
11		ベクトルの成分④ ①ベクトルａ→=（x,−1）、b→=（2,−3）に対して、v ａ→+3bとb→−ａ→が平行になるように実数xの値を定めよう。
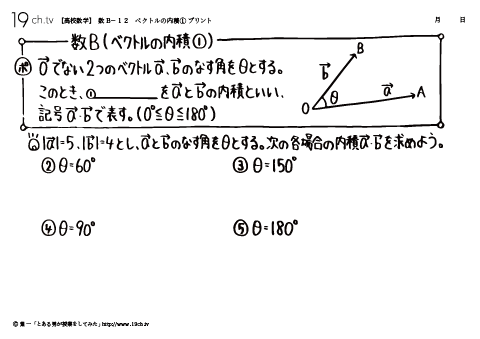
12		ベクトルの内積① 0→でない2つのベクトルa→、b→のなす角をθとする。このとき|a→| |b→|cosθをa→とb→の内積といい、記号a→・b→で表す。
13		ベクトルの内積② 右の図の直角三角形について、次の内積を求めよう。
14		ベクトルの内積③ ②a→=（4,5）、b→=（3,−2）の内積を求めよう。
15		ベクトルの内積④ ①a→=(k、k+1）、b→=（6、−4）が垂直となるように、kの値を求めよう。
16		ベクトルの内積⑤ 右の正六角形ABCDEFにおいて、AB=2とする。次の内積を求めよう。
17		ベクトルの内積⑥ ①|a→| =2、|b→|=1で、a→とb→のなす角が120°であるとき、3a→−2b→の大きさを求めよう。
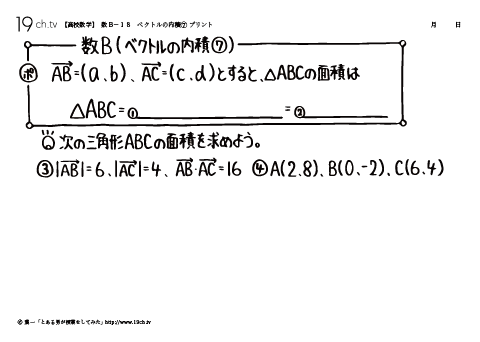
18		ベクトルの内積⑦ 次の三角形ABCの面積を求めよう。
19		ベクトルの内積⑧ ②不等式|a→・b→|≦|a→||b→|を証明しよう。

数B NO.20〜

NO.	イメージ	授業の内容	pdf
20		位置ベクトル① 2点A、Bを結ぶ線分ABについて、次の点の位置ベクトルをa→、b→で表そう。
21		位置ベクトル② △ABCの辺AB、BCを3：2に内分する点をそれぞれD、EACの中点をF△ABCの重点をGとする。次のベクトルをAB→=b→、AC=C→で表そう。
22		位置ベクトル③ △ABCと点Pについて3AP→+5BP→+4CP→=0→を満たす。
23		ベクトルと図形① 3点、P、R、Cが一直線上にあることを証明しよう。
24		ベクトルと図形② ○a→キ0→、b→キ0→、a→  bとする。次の等式を満たす実数S、tの値を求めよう。
25		ベクトルと図形③ AB→=b→、AC→=C→とするとき、AF→をb→、C→を 用いて表そう。
26		ベクトル方程式① 次の点Aを通り、d→が方向ベクトルである直線の媒介変数表示を、媒介変数tを用いて求めよう。また、tを消去した直線の方程式を求めよう。
27		ベクトル方程式② 次の2点を通る媒介変数表示を、媒介変数tを用いて求めよう。また、tを消去した直線の方程式を求めよう。
28		ベクトル方程式③ 次の点Aを通り、n→が法線ベクトルである直線の方程式を求めよう。
29		ベクトル方程式④ 次の円の方程式をベクトル方程式を利用して求めよう。

数B NO.30〜

NO.	イメージ	授業の内容	pdf
30		ベクトル方程式⑤ ①点A（1,−3）を通り、d→=（2,6）に平行な直線と垂直な直線の方程式を求めよう。
31		ベクトル方程式⑥ ①A（−1,5）、B(3,3）とする。線分ABの垂直二等分線の方程式を求めよう。
32		平面上の点の存在位置① ④△OABに対し、OP→=S OA→+t OB→とする。実数S、tが、S+t=3、S≧0、t≧0を満たしながら動く点Pの存在範囲を図示しよう。
33		平面上の点の存在位置② 実数S、tが次の条件を満たしながら動くとき、点Pの存在範囲を図示しよう。
34		平面上の点の存在位置③ 実数S、tが次の条件を満たしながら変化するとき、点Pの存在範囲を 図示しよう。
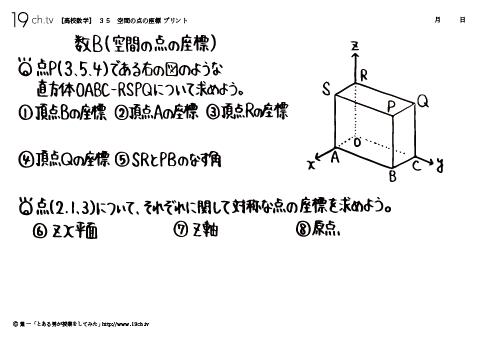
35		空間の点の座標 点P（3、5、4）である右の図のような直方体OABC-RSPQについて求めよう。
36		２点間の距離① 次の2点間の距離を求めよう。②A（2、−1、3）、B（4、3、−1）
37		２点間の距離② ①2点間A（1、2、−3）、B（3、－1、－4）から等距離にあるx軸上の点Pを求めよう。
38		空間ベクトルと成分① 平行六面体ABCD−EFCHにおいて、AB→=a→、 AD→=b→AE→=c→とする。次のベクトルa→、b→、c→を用いて表そう。
39		空間ベクトルと成分② 次のベクトルの大きさを求めよう。①a→=（4、−5、－3）

数B NO.40〜

NO.	イメージ	授業の内容	pdf
40		点の座標とベクトルの成分 A=（1、2、－1）、B（0、3、2）、C（5、－1、4）のとき、 次のベクトルの成分で表し。その大きさを求めよう。
41		空間ベクトルの内積① 右の図の直方体ABCD-EFGHは、AD=AE=1、AB=√3である。この直方体において、次の内積を求めよう。
42		空間ベクトルの内積② ①2つのベクトルa→=（0,2,1）、b→=（2,−2,1）に垂直で、大きさが3であるベクトルP→を求めよう。
43		空間ベクトルの内積③ AB⊥BC、AB⊥BDであることを示し、四面体ABCDの体積を求めよう。
44		空間ベクトルの内積④ ①x→=a→+tb→のうちで、大きさが最小となるx→を求めよう。
45		位置ベクトルと図形① 点P、点Q、点Rの位置ベクトルをa→、b→、c→、d→で表そう。
46		位置ベクトルと図形② 線分AEと線分CDの交点をPとするとき、OP→をOA→=a→、OB→=b→、OC→=c→を用いて表そう。
47		位置ベクトルと図形③ ①3点A（4,3,a）、B（2,－1,5）、C（5,b,－13）が一直線上に あるようにa、bの値を定めよう。
48		位置ベクトルと図形④ 平面DEFと線分OQの交点をRとするとき、OR：OQを求めよう。
49		位置ベクトルと図形⑤ ○四面体OABCと点Pについて、7OP→+2AP→+4BP→+5CP→=O→が成り立つ。

数B NO.50〜

NO.	イメージ	授業の内容	pdf
50		座標空間における図形① 3点A（8,－7,5）、B（－2,3,－5）、C（3,－2,－3）に対して、 次の各点の座標を求めよう。
51		座標空間における図形② 点A（5,－4,7）を通る、次のような平面の方程式を求めよう。
52		座標空間における図形③ ①（x+5)2+（y−1)2+（x－2)2=13がzy平面と交わってできる図形の方程式を求めよう。
53		空間における平面・直線の方程式① ①A（1,2,3）を通る、n→=（2,−1,－2）に 垂直な平面の方程式を求めよう。
54		空間における平面・直線の方程式② 次のような直線の方程式を媒介変数tを用いて表そう。
55		空間における平面・直線の方程式③ ①直線l：x=－1+t、y=3+t、z=1+2t上に点Pがある。 線分OPの最小となる点Pの座標を求めよう。
56		数列とは？ 数列を作っている各数を項という。その中でも最初のものを初項、最後のものを末項という。
57		等差数列とその和① 各項に一定の数dを加えると、次の項が得られるとき、この数列を等差数列といい、dを公差という。
58		等差数列とその和② ①初項3，公差4の等差数列において、47となる項は第何項が求めよう。
59		等差数列とその和③ ①第2項が80、第7項が65である等差数列は、第何項で初めて負の数になるかを求めよう。

数B NO.60〜

NO.	イメージ	授業の内容	pdf
60		調和数列 各項の逆数を項とする数列｛1/an｝が等差数列になるとき、｛an｝を調和数列という。
61		等差数列とその和④ 初項a、公差d、末項l、項数nの等差数列の和をSnとするとSn=1/2n（a+l)=1/2n｛2a+(n－1)d｝
62		等差数列とその和⑤ ①自然数の数列の和1+2+3+・・・+nを求めよう。
63		等差数列とその和⑥ 1から200までの整数のうち、次のような数の和を求めよう。
64		等差数列とその和⑦ 等差数列｛an｝は第5項が100、第10項が85である。
65		等比数列とその和① 各項に一定の数rを掛けると、次の項が得られるとき、この数列を等比数列といい、rをその公比という。
66		等比数列とその和② ①初項3、公比−2の等比数列の第5項を求めよう。
67		等比数列とその和③ ①数列−5、a、bが等差数列、数列a、b、45が等比数列をなすとき、a、b、の値を求めよう。
68		等比数列とその和④ 次の等比数列の初項から第n項までの和と第5項までの和を求めよう。
69		等比数列とその和⑤ 次の等比数列の初項と公比を求めよう。

数B NO.70〜

NO.	イメージ	授業の内容	pdf
70		等比数列とその和⑥ ①初項2、公比3の等比数列について、初項から第何項までの和が 初めて1000より大きくなるか求めよう。
71		複利計算 ①毎年初めにx円ずつ積み立てて、5年間で10万円にするには、何円ずつ貯金すればよいか求めよう。
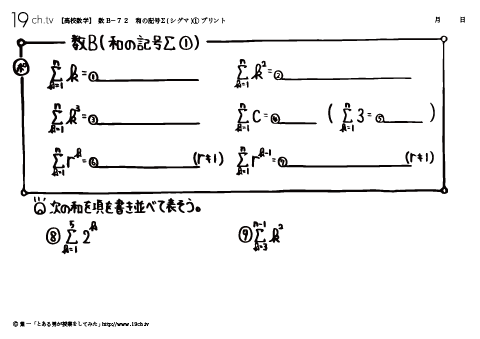
72		和の記号Σ(シグマ)① 次の和を項を書き並べ表そう。
73		和の記号Σ(シグマ)② 次の和を求めよう。
74		和の記号Σ(シグマ)③ 次の数列の第k項、および初項から第n項までの和を求めよう。
75		階差数列① 数列｛an ｝の隣り合う2つの項の差bn=an+1-an(n=1.2.3・・・）を項とする数列｛bn ｝を、数列｛an ｝の階級数列という。
76		階差数列② 次の数列の一般項を求めよう。 ①10、8、4、－2、－10
77		階差数列③ ①数列1、2、4、9、19、36、・・・・の一般項を求めよう。
78		数列の和と一般項① 数列｛an｝の初項から第n項までの和をSnとすると、a1=S1、 n≧2のとき　an=Sn－Sn-1
79		数列の和と一般項② 初項から第n項までの和が次の式で表される｛an｝の一般項を求めよう。

数B NO.80〜

NO.	イメージ	授業の内容	pdf
80		いろいろな数列の和① 次の数列の初項から第n項までの和を求めよう。①3、5・2、7・22、9・23・・・
81		いろいろな数列の和② 次の数列の初項から第n項までの和を求めよう。
82		いろいろな数列の和③ ①1/1+√2、1/√2+√3、1/√3+√4・・・
83		群数列① ①第7群の初めての数と終わりの数を求めよう。
84		群数列② ①第n群の奇数の和を求めよう。
85		群数列③ ②この数列の第200項を求めよう。
86		群数列④ ①22分の5は第何項か求めよう。
87		漸化式① 次の条件で定められる数列のa2、a5を求めよう。
88		漸化式② 次の条件で定められる数列｛an｝の一般項を求めよう。
89		漸化式③ ①a1=1、an+1=3an−2

数B NO.90〜

NO.	イメージ	授業の内容	pdf
90		漸化式④ ①a1=1、an+1=3an+4n
91		漸化式⑤ 次の条件で定められる数列｛an｝の一般項を求めよう。
92		漸化式⑥ ①a1=2、a(n+1)=2an+2(n−1)
93		漸化式⑦ ①a1=3、a2=5、an+2-3an+1+2an=0
94		漸化式⑧ 数列｛an+bn｝、｛an-bn｝の一般項を求めよう。
95		数学的帰納法① ①12+22+32+・・・・n2=1/6n(n+1)(2n+1)を数学的に帰納法によって証明しよう。
96		数学的帰納法② ①nを自然数とするとき、11n-1は10の倍数であることを、 数学的帰納法によって証明しよう。
97		数学的帰納法③ ①nを自然数とするとき、3n+2＞10n+12を数学的帰納法によって証明しよう。
98		数学的帰納法④ ①n≧10を満たす自然数nに対して、2n＞10n2が成り立つことを数学的帰納法によって証明しよう。
99		数学的帰納法⑤ ①a1=2、an+1=2-1/an(n=1、2、3、・・・）で定義される数列｛an｝について、 一般項anを推測し、それが正しいことを、数学的帰納法を用いて証明しよう。

数B NO.100〜

NO.	イメージ	授業の内容	pdf
100		数学的帰納法⑥ ①nが自然数のとき、3^nと5n+1の大小をお比較しよう。
101		確率分布と確率変数① 2個のさいころを同時に投げて、出る目の差をxとする。①xの確率分布を求めよう。
102		確率分布と確率変数② ①1個のさいころを3回投げるとき、出た目の最大値xの確率分布を求めよう。
103		期待値① 次の確率変数Xの期待値を求めよう。①白玉5個と黒玉3個が入った袋から3個の玉を同時に取り出すとき、その中に含まれる黒玉の個数Xほか。
104		期待値② ①1個のさいころを投げ、「出た目の数×500円」を受け取るゲームをする。
105		分散と標準偏差 確率変数Xの確率分布が右の表で与えられるとき、 次の値を求めよう。
106		確率変数の和と積① ①2枚の硬貨を同時に投げる試行を2回行う。1回目の試行で表の出る枚数をX、2回目の試行で表の出る枚数をYとすとき、XとYの同時分布を求めよう。
107		確率変数の和と積② ①確率変数Xの期待値を求めよう。
108		確率変数の和と積③ 大中小3個のさいころを投げるとき、次の値を求めよう。①出る目の和の期待値
109		二項分布① 1個のさいころを5回投げて、3の倍数の目が出る回数をXとする。Xはどのような二項分布に従うか。また、次の確率を求めよう。

数B NO.110〜

NO.	イメージ	授業の内容	pdf
110		二項分布② 次の二項分布の平均、分散、標準偏差を求めよう。
111		二項分布③ 1個のさいころを100回投げて、3の倍数の目が出る回数をxとする。xの期待値、分散、標準偏差を求めよう。
112		正規分布① 確率変数Xの確率密度関数f(x)が、次の式で与えられたとき、指定された確率をそれぞれ求めよう。
113		正規分布② 確率変数Zが標準正規分布N(0、1）に従うとき、次の確率を求めよう。
114		正規分布③ 確率変数Xが正規分布N(2、52）に従うとき、次の確率を求めよう。
115		母集団と標本① 玉に書かれている数字の母集団分布を求めよう。
116		母集団と標本② P(1)=0.3413、P(2)=0,4772として、次の確率を求めよう。
117		推定 (最終回) 大きさ100の標本の平均値は56.3で標本標準偏差は10.2である。 このとき、母平均mに対して、信頼度95％の信頼区間を求めよう。

ページ上部へ戻る